Рисуем диаграммы Вольперта-Смита на Python
8 апреля 2020
Круговая диаграмма полных сопротивлений, она же диаграмма Вольперта-Смита или диаграмма Смита — это круговая диаграмма, часто используемая для отображения комплексного сопротивления чего бы то ни было. Одно из интересных свойств данной диаграммы заключается в том, что с ее помощью легко производить некоторые вычисления прямо на бумаге. Например, зная входное сопротивление антенны и рабочую частоту, нетрудно определить, как с помощью LC-схемы привести сопротивление к значению 50 Ом. Этим активно пользовались до появления персональных компьютеров, благодаря чему диаграмма Смита и обрела популярность. Давайте же попробуем порисовать диаграммы Смита на языке Python.
Для этого воспользуемся библиотекой pySmithPlot. Она в свою очередь зависит от Matplotlib и NumPy, про которые ранее уже рассказывалось в этом блоге. Чтобы не засорять систему кучей пакетов, воспользуемся virtualenv.
Итак, установка:
Здесь указана конкретная версия NumPy. На момент написания статьи у pySmithPlot была небольшая проблема с совместимостью с более поздними версиями. Имеется патч, но он еще не принят в апстрим. Вы можете использовать pySmithPlot с последней версией NumPy, но библиотеку придется скопировать в репозиторий вашего проекта и вручную применить патч.
Давайте сразу рассмотрим небольшую задачку. В рамках статьи Фильтры из коаксиального кабеля, часть 2 мы выяснили, как зависит входное сопротивление, которое мы видим на конце кабеля с волновым сопротивлением Z0, соединенного на втором конце с нагрузкой с сопротивлением ZL, от длины кабеля L:
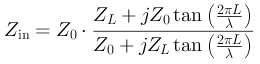
Здесь L измеряется в длинах волны λ. Естественно, в общем случае необходимо учитывать коэффициент укорочения кабеля. Так вот, допустим, мы используем кабель RG-6U+CU c Z0 = 75 Ом, и он соединен с антенной delta loop, имеющей ZL = 106 Ом. Требуется изобразить на диаграмме Смита, как будет меняться Zin на интервале L ∈ [0; λ/4].
Решение:
import numpy as np
from math import pi, tan
from matplotlib import pyplot as pp
from smithplot import SmithAxes
def zf(x):
z0 = 75
zl = 106
return z0*(zl+1j*z0*tan(x))/(z0+1j*zl*tan(x))
pp.figure(figsize=(6, 6))
ax = pp.subplot(1, 1, 1, projection='smith')
ax.update_scParams(axes_impedance = 50)
lam = np.linspace(0.0, 0.25, 8)
imp = np.vectorize(zf)(2*pi*lam)
pp.plot(imp, datatype="Z")
pp.savefig('./smith.png')
А вот так выглядит картинка на выходе:
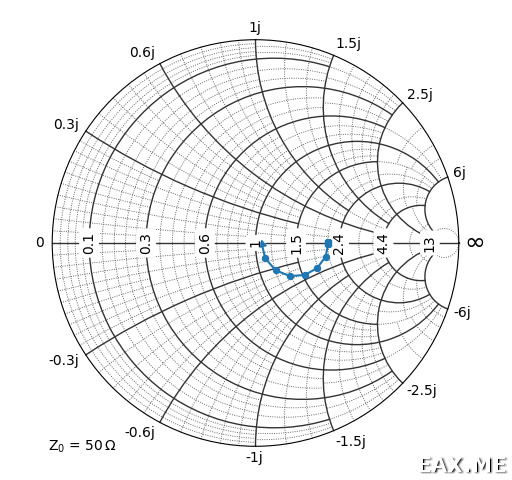
Видим, что при длине λ/4 кабель согласует 106 Ом антенны в почти идеальные 50 Ом, как и положенно четвертьволновому трансформатору.
Fun fact! Приведенная картинка наглядно иллюстрирует, почему балуны, использующие бифилярную обмотку, превосходно работают. Хотя, казалось бы, при использовании в балуне двухпроводной линии с волновым сопротивлением 150-300 Ом ничего хорошего ожидать не приходится. Если нагрузить такой балун на эквивалент нагрузки 50 Ом, то на условных 14 МГц мы действительно увидем КСВ 2. Однако ничто не мешает слегка подогнать размеры антенны, сделав ее входное сопротивление чуть-чуть реактивным. Отрезок двухпроводной линии в балуне преобразует это сопротивление в чисто активное, и антенна будет работать как надо. Заинтересованным читателям предлагается построить соответствующую диаграмму самостоятельно.
Это все, о чем я хотел сегодня рассказать. Больше примеров использования pySmithPlot вы найдете в репозитории проекта. Для желающих узнать больше о диаграммах Смита могу порекомендовать видео Basics of the Smith Chart, которое снял Alan Wolke, W2AEW.
Дополнение: Вас также могут заинтересовать посты Анализ антенного тюнера при помощи Python и Моделирование антенн на Python при помощи PyNEC.
Метки: Python, Беспроводная связь, Любительское радио.
Вы можете прислать свой комментарий мне на почту, или воспользоваться комментариями в Telegram-группе.