Записки программиста

В статье Режекторные фильтры из коаксиального кабеля мы познакомились с фильтрами из отрезка кабеля длиной λ/4. Существуют фильтры с похожим принципом действия, но представляющие собой два отрезка кабеля длиной λ/8. В английском языке эти фильтры иногда называют double stubs. Давайте же выясним, как эти фильтры работают.

Так как у меня подыссякли запасы кабеля RG213, фильтр было решено делать на радиолюбительский УКВ диапазон 2 метра (144-146 МГц):

С учетом коэффициента укорочения кабеля длина λ/8 отрезков составила 172 мм. Отрезки соединены параллельно, конец левого закорочен, а конец правого разомкнут. После пайки концы кабелей оборачиваем изолентой. В центральной части фильтра восстанавливаем экран кабеля по уже знакомой нам методе «слой изоленты, слой фольги, слой изоленты». Это позволяет улучшить АЧХ.

Спрашивается, на каких же частотах фильтр будет что-то фильтровать? Если мы увеличим нашу частоту 145 МГц в два раза, то на ней отрезки кабеля будут иметь длину λ/4. Закороченный λ/4 отрезок ничего не делает, но зато разомкнутый отфильтровывает сигнал. При увеличении частоты в четыре раза отрезки будут иметь длину λ/2. Теперь они меняются ролями — разомкнутый кабель бездействует, а закороченный отфильтровывает сигнал. Таким образом, будут отфильтрованы все четные гармоники.

Но будет ли потеряна какая-то часть энергии на основной частоте? Давайте выясним. Если внимательно присмотреться к приведенному выше фото, то можно кое-что заметить. Правый отрезок кабеля можно рассматривать как конденсатор, соединяющий жилу и экран кабеля. Аналогично левый отрезок представляет собой индуктивность. Спрашивается, а можем ли мы определить их импеданс? Оказывается, что можем. Кабель с волновым сопротивлением Z₀ и длиной L, соединенный с нагрузкой, имеющей импеданс Z_L, имеет вполне определенный импеданс:

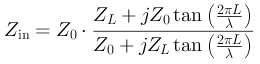
У нас L = λ/8. Соответственно, аргументом тангенса будет π/4, а tan(π/4) = 1. Теперь, чтобы определить импеданс закороченного кабеля, подставим в уравнение Z_L = 0, и получаем Z_in = j · Z₀ = 50j Ом. Чтобы определить импеданс разомкнутого кабеля, поделим числитель и знаменатель в уравнении на Z_L, после чего подставим Z_L = ∞. Получим Z_in = Z₀ · (1 / j) = -j · Z₀ = -50j Ом.

Занятно. Теперь, так как катушка и конденсатор соединены параллельно, их суммарный импеданс будет равен Z₁·Z₂/(Z₁+Z₂)… ой, получили бесконечность. Выходит, на основной частоте ток сюда вообще не потечет.

В общем и целом, здесь работает тот же принцип, что в простейшем полосно-пропускающем фильтре или в антенных трапах. На резонансной частоте параллельный LC-контур имеет высокий импеданс и ток по нему не течет.

Давайте же проверим наш фильтр при помощи анализатора спектра:

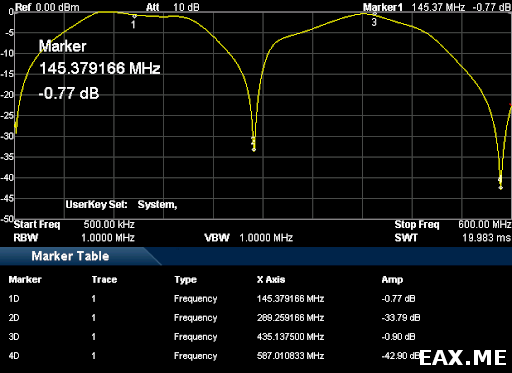
Видим, что на основной частоте, а также на нечетных гармониках, сигнал проходит. На четных гармониках сигнал подавляется. Если смотреть выше 600 МГц, то там кривая заметно портится. Это происходит как минимум по той причине, что UHF-разъемы не особо предназначены для работы на таких частотах (вообще-то, их не рекомендуется использовать выше 200-300 МГц). Кроме того, согласование импеданса в центре нашего фильтра оставляет желать лучшего — пайка, фольга, изолента, вот это вот все.

Рассмотрим левую половину кривой поближе:

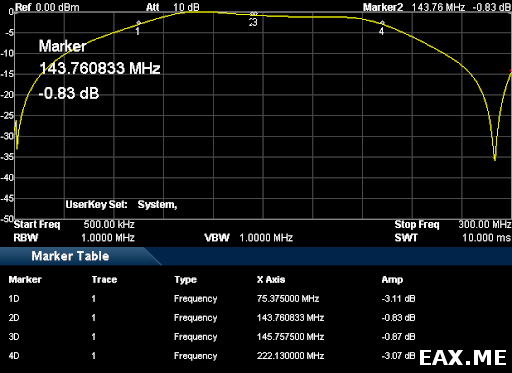
АЧХ в полосе пропускания получилась не совсем ровной. В частности, на радиолюбительском диапазоне 2 м, 144-146 МГц, сигнал проходит с аттенюацией около -0.85 дБ. Это соответствует 1-pow(10,-0.85/10) или 17.8% потери мощности. Не мало, однако для фильтров это все еще считается приемлемым результатом.

Перейдем к правой половине кривой:

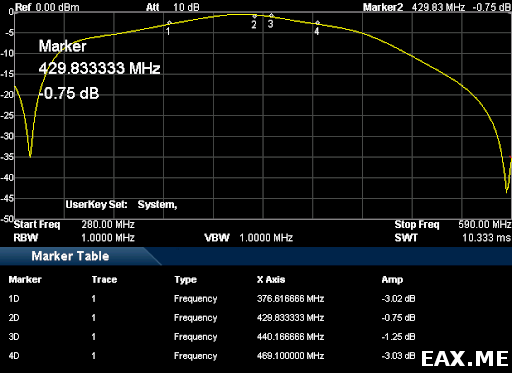
В радиолюбительском диапазоне 70 см, 430-440 МГц, аттенюация составляет от -0.75 дБ в начале диапазона до -1.25 дБ в его конце, что соответствует 15.9% и 25% потери мощности. Это уже многовато. Для каких-то задач фильтр не подойдет. Стоит однако отметить, что ни на одном из диапазонов мною не предпринималось никаких попыток подстроить фильтр.

Обратите внимание, что в «провалах» у этого фильтра мы видим -35..-40 дБ. У простого фильтра из λ/4 отрезка кабеля мы видели порядка -26..-28 дБ. Правда, тот фильтр был на КВ. Для чистоты эксперимента следовало бы сравнивать два КВ или два УКВ фильтра. Заинтересованные читатели могут произвести такое сравнение в качестве упражнения.

А еще в этот фильтр можно добавить переключатель, отсоединяющий разомкнутый кабель. Останется закороченный отрезок кабеля, имеющий длину λ/4 на частоте 2*F, где F в нашем случае была 145 МГц. Как нам уже известно, такой фильтр будет вырезать частоты 2*(2*F), 4*(2*F) и так далее, в общем, все четные гармоники частоты 2*F. Данный эксперимент также предлагается читателям в качестве упражнения.

Дополнение: Фильтры из коаксиального кабеля, часть 3

Метки: Беспроводная связь, Любительское радио, Электроника.