Моделирование антенн на Python при помощи PyNEC
29 марта 2021
NEC2++ — это движок для моделирования антенн, совместимый с NEC2. Движок написан на C++ и распространяется под лицензией GPL. Также предусмотрены байндинги к языку Python. О них далее и пойдет речь.
Для экспериментов нам понадобятся следующие пакеты:
Во избежание конфликтов между пакетами и чтобы не засорять систему, рекомендую использовать virtualenv. PyNEC указан конкретной версии по той причине, что в самой последней версии на момент написания статьи был открытый баг. Он делал использование пакета невозможным. К моменту, когда вы будете читать эти строки, баг может быть устранен.
Моделировать будем антенну inverted-V на диапазон 20 метров, установленную на 10-и метровой мачте. У нас будет несколько скриптов, анализирующих разные свойства антенны. Общий код положим в файл common.py:
from math import pi, sin
def free_space(nec):
# 0 - no ground plane
# 1 - ground plane with current expansion
# -1 - ground plane without current expansion
nec.geometry_complete(0)
def good_ground(nec):
conductivity = 0.0303 # S/m
rel_dielectric_constant = 20.0
nec.geometry_complete(1)
nec.gn_card(0, 0, rel_dielectric_constant, conductivity,
0, 0, 0, 0)
def average_ground(nec):
conductivity = 0.005 # S/m
rel_dielectric_constant = 13.0
nec.geometry_complete(1)
nec.gn_card(0, 0, rel_dielectric_constant, conductivity,
0, 0, 0, 0)
def poor_ground(nec):
conductivity = 0.001 # S/m
rel_dielectric_constant = 3.0
nec.geometry_complete(1)
nec.gn_card(0, 0, rel_dielectric_constant, conductivity,
0, 0, 0, 0)
def geometry(length=5.22, angle=100, height=10, nr_segments=21,
ground=average_ground):
nec = PyNEC.nec_context()
nec.set_extended_thin_wire_kernel(False)
wire_radius = 0.0005 # 0.5 mm
length_ratio = 1.0
radius_ratio = 1.0
eps = 0.1
b = length*sin(pi*angle/2/180)
a = length*sin(pi*(90 - angle/2)/180)
geo = nec.get_geometry()
# center
geo.wire(1, 1, 0, -eps, height, 0, eps, height,
wire_radius, length_ratio, radius_ratio)
# left
geo.wire(2, nr_segments, 0, -b, height-a, 0, -eps, height,
wire_radius, length_ratio, radius_ratio)
# right
geo.wire(3, nr_segments, 0, b, height-a, 0, eps, height,
wire_radius, length_ratio, radius_ratio)
ground(nec)
# voltage excitation in the center of the antenna
segment_nr = 1
voltage = 1.0+0j
ex_voltage_excitation = 0
nec.ex_card(ex_voltage_excitation, segment_nr, 1, 1,
voltage.real, voltage.imag, 0, 0, 0, 0)
return nec
Здесь основная функция — это geometry. Она возвращает объект nec_context. Объект имеет N-ое количество методов-оберток к движку, а также хранит стейт с информацией о свойствах земли, проводах, из которых состоит антенна, и что именно в ней нужно промоделировать.
Не могут не бросаться в глаза странные имена методов, вроде gn_card и ex_card. Эта терминология позаимствована из движка NEC2. Движок принимает на вход файл, содержащий строки в определенном формате. Файл в терминологии NEC2 называется колодой (deck), а строки в нем — картами (card). Нужно понимать, что история NEC2 уходит корнями во времена, когда программисты писали на Fortran и работали с перфокартами. Отсюда и такая терминология.
Так вот, допустим, мы хотим описать землю. Для этого в файл нужно добавить строчку GN (какие-то аргументы). Говорят, что это GN-карта. Описание всех возможных карт, ровно как и их аргументов, можно найти в документации на NEC2. Пример колоды есть на Википедии. Еще в cocoaNEC можно открыть вкладку «Cards» и посмотреть, в какую колоду был странслирован код на NC.
Обладая этой информацией, код перестает казаться таким уж запутанным. Здесь мы объявили четыре варианта земли. Аргументы для GN-карт были банально подсмотрены в cocoaNEC. Далее в функции geometry мы рисуем inverted-V из трех проводов (geo.wire), подстилаем под ними землю, и говорим, что антенна питается в первый сегмент провода с меткой «1» (nec.ex_card).
Имея модель антенны, какая идея первой приходит на ум? Конечно же, построить график КСВ:
import matplotlib.pyplot as plt
import PyNEC
from common import *
def vswr(z, z0):
Gamma = abs((z - z0) / (z + z0))
return float((1 + Gamma) / (1 - Gamma))
nec = geometry()
system_impedance = 50
count = 100
start_freq = 13.8
stop_freq = 14.6
step_size = (stop_freq - start_freq) / count
ifrq_linear_step = 0
nec.fr_card(ifrq_linear_step, count, start_freq, step_size)
nec.xq_card(0) # execute simulation
freqs = []
vswrs = []
for idx in range(0, count):
ipt = nec.get_input_parameters(idx)
z = ipt.get_impedance()
freqs.append(ipt.get_frequency() / 1000000)
vswrs.append(vswr(z, system_impedance))
dpi = 80
plt.figure(dpi = dpi, figsize = (512 / dpi, 384 / dpi) )
plt.plot(freqs, vswrs)
plt.title("SWR vs Frequency")
plt.xlabel("Frequency, MHz")
plt.ylabel("SWR")
plt.axis([start_freq, stop_freq, 1.0, 3.0])
plt.grid(True)
plt.savefig("swr.png")
Здесь FR-карта задает интервал частот, на котором будет анализироваться антенна, а XQ-карта запускает моделирование. В итоге мы получаем данные для 100 частот с шагом 8 кГц. Для каждой частоты определяется входное сопротивление антенны. Из него вычисляется КСВ, график которого нам и нужен. График рисуется при помощи библиотеки Matplotlib.
Результат:
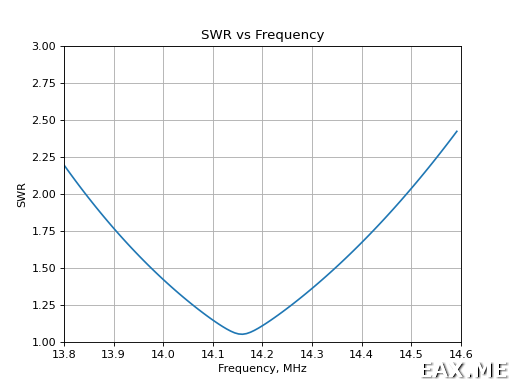
С тем же успехом входное сопротивление антенны можно отобразить на диаграмме Вольперта-Смита. Заинтересованным читателям предлагается модифицировать скрипт соответствующим образом в качестве упражнения.
Казалось бы, на КСВ можно остановиться, но уж нет! Раз есть модель антенны, то нарисуем полярную диаграмму ее усиления под углом 33° к горизонту на середине телеграфного участка:
import matplotlib.pyplot as plt
import PyNEC
from common import *
nec = geometry()
freq_mhz = 14.035
ifrq_linear_step = 0
nec.fr_card(ifrq_linear_step, 1, freq_mhz, 0)
elevation = 33
theta_angle = 90 - elevation
nec.rp_card(calc_mode=0, n_theta=1, n_phi=360,
output_format=1, normalization=0, D=0, A=0, # XNDA = 1000
theta0=theta_angle, phi0=0, delta_theta=0, delta_phi=1,
radial_distance=5000, gain_norm=0)
nec.xq_card(0) # execute simulation
rpt = nec.get_radiation_pattern(0)
gain = rpt.get_gain_tot()
gm = max(gain)
xs = [2*pi*float(phi)/360 for phi in range(gain.size)]
ys = [-36 if g-gm < -36 else g-gm for g in gain]
dpi = 80
fig = plt.figure(dpi = dpi, figsize = (512 / dpi, 384 / dpi) )
ax = plt.subplot(111, projection='polar')
ax.set_title('Elevation {} deg'.format(elevation))
ax.set_xlabel('Max gain: {:.2f} dBi'.format(gm))
ax.plot(xs, ys, linestyle = 'solid', color='red')
ax.set_rmax(0)
ax.set_rticks([-6*i for i in range(0,7)])
ax.set_yticklabels([''] + [str(-6*i) for i in range(1,7)])
ax.set_theta_direction(-1)
ax.set_rlabel_position(-90)
ax.set_thetagrids(range(0, 360, 15))
ax.grid(True)
fig.savefig('elevation.png')
FR-карта в этот раз задает одну, фиксированную частоту. За диаграмму направленности отвечает RP-карта. В этой карте нужно указать начальные значения углов phi и theta в сферической системе координат, с каким шагом и сколько раз они будут обновляться, плюс некоторые другие параметры. Заметьте, что зениту соответствует theta = 0. В итоге для всех пар (phi, theta) получаем усиление антенны в dBi. Его остается только отобразить на полярной диаграмме. Сталкиваться с последней нам уже доводилось:
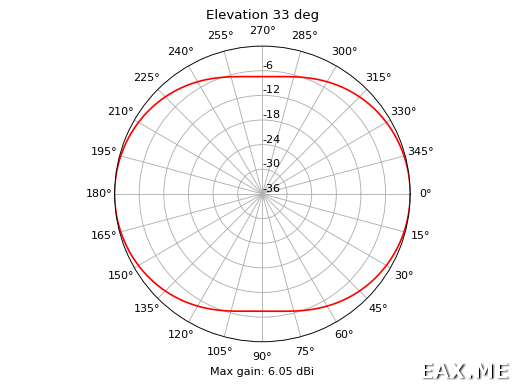
И для полноты картины построим аналогичную диаграмму для фиксированного азимута и переменной элевации:
import matplotlib.pyplot as plt
import PyNEC
from common import *
nec = geometry()
freq_mhz = 14.035
ifrq_linear_step = 0
nec.fr_card(ifrq_linear_step, 1, freq_mhz, 0)
azimuth = 0
nec.rp_card(calc_mode=0, n_theta=181, n_phi=1,
output_format=1, normalization=0, D=0, A=0, # XNDA = 1000
theta0=-90, phi0=azimuth, delta_theta=1, delta_phi=0,
radial_distance=5000, gain_norm=0)
nec.xq_card(0) # execute simulation
rpt = nec.get_radiation_pattern(0)
gain = rpt.get_gain_tot()
gm = max(gain)
xs = [2*pi*float(90-theta)/360 for theta in range(gain.size)]
ys = [-36 if g-gm < -36 else g-gm for g in gain]
dpi = 80
fig = plt.figure(dpi = dpi, figsize = (512 / dpi, 384 / dpi) )
ax = plt.subplot(111, projection='polar')
ax.set_title('Azimuth {} deg'.format(azimuth))
ax.set_xlabel('Max gain: {:.2f} dBi'.format(gm))
ax.set_thetamin(-90) # set the limits
ax.set_thetamax(90)
ax.set_theta_offset(2*pi*90/360)
ax.plot(xs, ys, linestyle = 'solid', color='red')
ax.set_rmax(0)
ax.set_rticks([-6*i for i in range(0,7)])
ax.set_yticklabels([''] + [str(-6*i) for i in range(1,7)])
ax.set_thetagrids(range(-90, 91, 15))
ax.set_theta_direction(-1)
ax.grid(True)
fig.savefig('azimuth.png')
Результат:
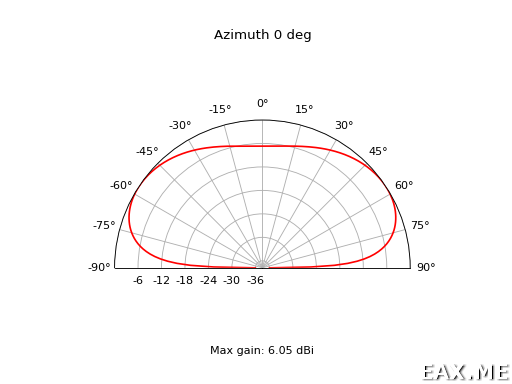
Диаграмма выглядит немного непривычно. Дело в том, что масштаб на ней, как и на предыдущей диаграмме, линейный. Но в книгах и в антенных моделировщиках мы привыкли видеть логарифмический масштаб. Заинтересованным читателям предлагается устранить этот дефект в качестве упражнения. Также в качестве упражнения предлагается нарисовать диаграмму направленности антенны в 3D. Полную версию исходников вы найдете на GitHub.
При помощи PyNEC могут быть решены разные задачи. Например, его можно использовать для оптимизации антенн по заданному критерию. Кроме того, библиотека может послужить основой для кроссплатформенного антенного моделировщика.
Дополнение: Пример практического применения PyNEC описан в заметке Антенна ZS6BKW на пять КВ-диапазонов.
Метки: Python, Антенны, Беспроводная связь, Любительское радио.
Вы можете прислать свой комментарий мне на почту, или воспользоваться комментариями в Telegram-группе.