Записки программиста

Иногда нужно знать точные характеристики кварцевого резонатора. Но даже если у вас есть даташит на конкретный кварцевый резонатор, в нем вы никогда не найдете нужную информацию. В силу производственных процессов даже два кварца из одной партии сильно отличаются друг от друга. Остается лишь один вариант — научиться измерять кварцы самостоятельно.

Примечание: Вас также могут заинтересовать статьи Определяем добротность и частоту собственного резонанса катушки индуктивности и Как опознать неизвестное ферритовое кольцо, если вдруг вы их пропустили.

Рассмотрим эквивалентную схему кварцевого резонатора:

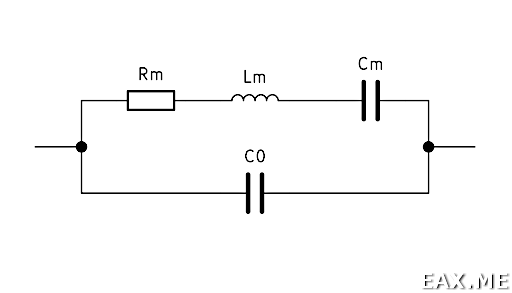
Здесь C0 — это собственная емкость резонатора. Она образуется электродами, идущими к кристаллу. Lm и Cm — эквивалентные индуктивность и емкость резонатора. Rm представляет собой сопротивление потерь. Задача состоит в том, чтобы измерить эти четыре параметра.

Соответствующие методы измерений описаны во многих источниках, включая книги The ARRL Handbook, Experimental Methods in RF Design и QRP Power. Alan Wolke, W2AEW недавно опубликовал видео Measuring crystals with NanoVNA and other tools, где он показывает и сравнивает различные методы. Для большинства измерений Alan использует NanoVNA. Здесь я расскажу о том, как сам измеряю кварцы на примере случайного резонатора на 12 МГц под брендом «CALTRON». Дополнительную информацию вы найдете в названных книгах и видео.

Проще всего определить C0. Для этого достаточно измерить резонатор с помощью RLC-метра в режиме измерения емкости. В моем случае C0 = 2.5 пФ.

Для измерения Lm и Cm воспользуемся методом Dr. Dave Gordon-Smith, G3UUR. Это самый распространенный метод, и среди бюджетных вариантов он считается наиболее точным. Нам понадобится следующий генератор:

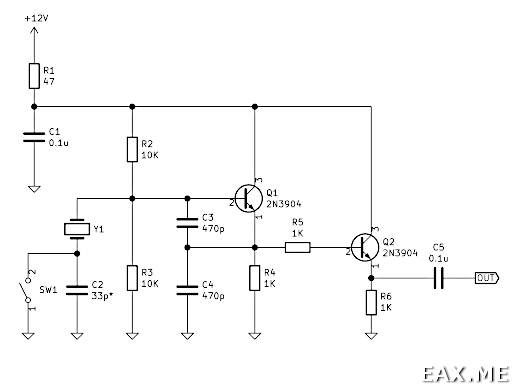
Номиналы C2, C3 и C4 не критичны. Должны выполняться условия C3 = C4 и C2 << С3. Чаще всего используются C2 = 33 пФ, C3 = C4 = 470 пФ. У меня не было конденсатора на 33 пФ, поэтому я использовал на 22 пФ.

Генератор в моем исполнении:

Чтобы постоянно не припаивать и не отпаивать кварцы, были использованы гнезда с шагом 2.54 мм. Когда генератор готов, нужно измерить C2 вместе со всеми паразитными эффектами. У меня окончательное значение составило 26.5 пФ.

Измеряемый кварц помещается в генератор, после чего определяются две частоты. Частота генератора Fo, когда переключатель SW1 разомкнут, и Fg, когда переключатель замкнут. Для получения точных результатов нужен частотомер. Для менее точных измерений может быть использован осциллограф или SDR-приемник.

Далее Lm и Cm вычисляются по формулам:

Например:

Итого, Cm = 9.678 фФ (фемтофарад), Lm = 18.183 мГн (миллигенри).

Для определения Rm необходимо измерить АЧХ последовательно включенного кварца в окрестностях резонансной частоты. Для этого было изготовлено такое незамысловатое устройство из двух BNC-разъемов и гнезд с шагом 2.54 мм:

Анализатор спектра должен показать что-то вроде:

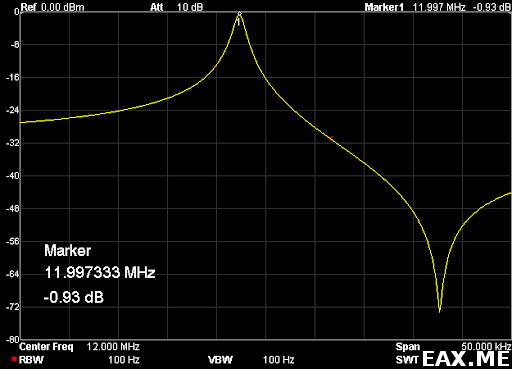
Наша задача — как можно точнее определить вносимые потери на резонансной частоте. На этой частоте Lm и Cm компенсируют друг друга, и потери приходятся в основном на Rm. Опытным путем было установлено, что Span в 50 кГц и RBW 100 Гц дают достаточно точный результат.

Rm можно вычислить по формулам:

Пример:

Получили 11.3 Ом.

Зная Lm, Rm и резонансную частоту, мы также можем вычислить добротность кварцевого резонатора:

Добротность нашего кварца:

Хорошие кварцевые резонаторы имеют добротность не менее 100 000. Данный кварц является довольно неплохим.

Fun fact! Параллельное соединение двух кварцевых резонаторов, как в схеме Super VXO, эквивалентно использованию одного кварцевого резонатора меньшей добротности. Для наших кварцев получаем C0 = 5 пФ, Cm = 19.329 фФ, Lm = 9.104 мГн, Rm = 8.9 Ом, Q = 77 000. Также параллельное соединение как бы «сглаживает» пик на последнем графике. На самом деле, будет два пика на близких частотах.

Итак, мы определили Lm, Cm, Rm и C0, а также посчитали добротность. Осталось только понять, какая от этого практическая польза. Но на этот вопрос я намерен ответить в одном из будущих постов. Следите за обновлениями.

Дополнение: См также заметки про кварцевые полосовые фильтры, часть 1, часть 2, часть 3 и часть 4.

Метки: Электроника.