Записки программиста

Любой, кто пробовал читать книги о SDR и DSP, наверняка встречал формулы с комплексными числами, загадочные спирали в трехмерном пространстве, а также какие-то отрицательные частоты. Нередко авторы чрезмерно увлекаются математическими формулами, из-за чего понять происходящее, а также его связь с физическим миром, не так-то просто. Попробуем во всем разобраться.

Отмечу, что я не претендую на звание выдающегося математика. Все написанное ниже — не более, чем мое дилетантское понимание применительно к одной конкретной интересующей меня предметной области, радио. Если вы серьезный математик и видите ошибки в тексте, не стесняйтесь сообщить мне о них.

Приведенные ниже иллюстрации были позаимствованы из 8-ой главы книги Understanding Digital Signal Processing, 3rd Edition, автор Richard Lyons. Это очень хорошая книга. Если вы серьезно интересуетесь цифровой обработкой сигналов, вам стоит ознакомиться с ней целиком.

Итак, рассмотрим комплексную плоскость:

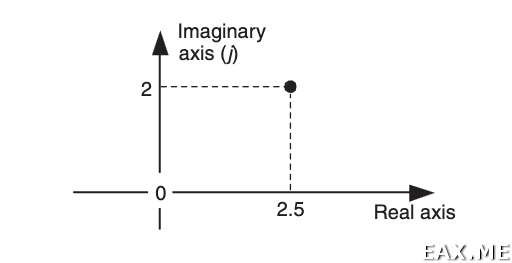
Перед нами графическое представление комплексного числа 2.5 + j2. Можно думать о нем, либо как о точке в двумерном пространстве, либо как о векторе, соединяющим начало координат с этой точкой. Аналогия с вектором условная. В частности, произведение векторов не имеет ничего общего с произведением комплексных чисел.

Спрашивается, что такое j или мнимая единица? Это такая абстрактная штука, умножение на которую приводит к повороту вектора (или точки) в комплексной плоскости на 90°:

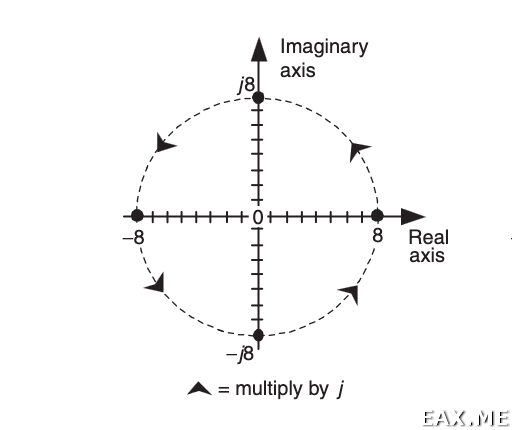
Здесь показан результат умножения вещественного числа 8 на мнимую единицу. Первое умножение дает нам:

… что и вправду является поворотом на 90°. Второе умножение:

… и так далее.

Из последнего уравнения получается, что j — это как будто бы квадратный корень из −1. Впрочем, такое определение скорее запутывает, чем действительно что-то объясняет. Аналогичным образом, умножение на −j означает поворот на −90°.

Благодаря трудам барона Фурье мы знаем, что любая периодическая функция может быть разложена в ряд тригонометрических функций. Сегодня мы называем такое разложение спектром сигнала. До Фурье существование какого-то спектра было совершенно неочевидным. Сейчас же радиолюбители воспринимают его, как что-то само собой разумеющееся.

Существует важнейшая связь между тригонометрическими функциями и комплексной экспонентой:

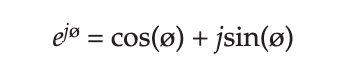
Это формула Эйлера. Она может быть доказана через разложение функций в ряды Тейлора:

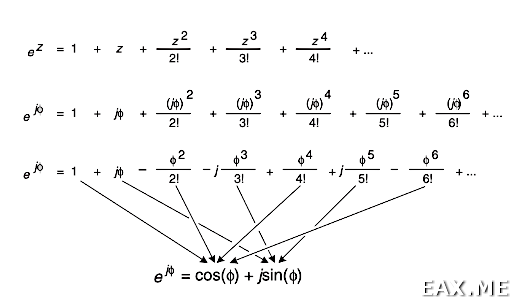
Благодаря формуле Эйлера синус и косинус могут быть выражены через комплексные экспоненты. Что фактически является представлением данных функций в частной области. Зная это, можно понять работу преобразования Гильберта. Однако сей вопрос уже выходит за рамки поста.

Рассмотрим случай, когда есть не просто точка на комплексной плоскости, а изменяющийся во времени сигнал. Соответственно, нам понадобится еще одна ось — ось времени. График при этом становится трехмерным:

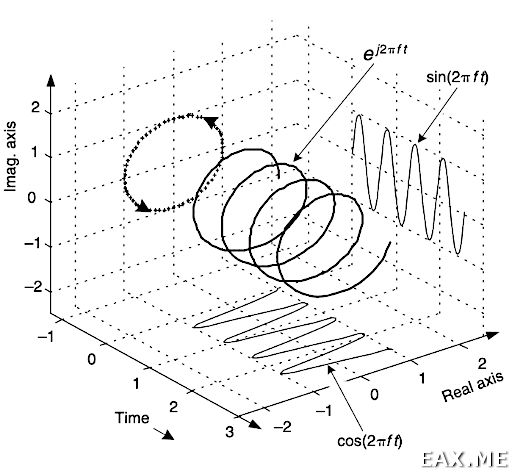
Здесь f — это частота колебаний в герцах. Давайте пристально посмотрим на получившуюся картинку. Ничего не напоминает?

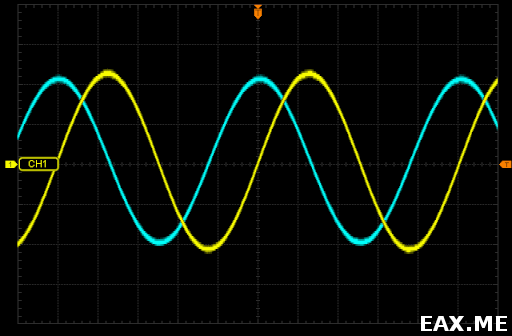
Да это же синфазный (I) и квадратурный (Q) сигналы на выходе квадратурного демодулятора. А чтобы получить круг, сигналы нужно подать на осциллограф в режиме X-Y.

Фактически, в квадратурном демодуляторе происходит комплексное умножение на сигнал гетеродина. Чтобы убедиться в этом, смотрим на структурную схему квадратурного демодулятора, а затем на формулу Эйлера.

Занимательный факт. Умножение некого исходного сигнала e^j2πf₀ на сигнал гетеродина e^j2πft равносильно переносу сигнала на f герц вверх по частоте. Умножение на e^−j2πft равносильно переносу вниз.

В этом несложно убедиться, если вспомнить, что при перемножении степеней с одинаковым основанием показатели складываются. Получается «идеальный смеситель». Вместо суммы и разности двух частот, как в простом смесителе, он дает либо только сумму, либо только разность, смотря что мы хотим.

Обладая этой информацией, можно понять, как работает преобразование Фурье:

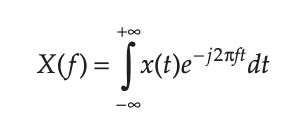
В нем исходный сигнал x(t) умножается на e^−j2πft, что переносит заданную частоту f на 0 Гц. Затем получившийся сигнал x′(t) интегрируется по времени от −∞ до +∞. Так так сигнал периодический, интегрирование дает нам ноль, плюс постоянную составляющую. Мы только что перенесли туда f. Что дает отклик на заданной частоте.

Вдумчивый читатель мог заметить, что в формуле e^−j2πft у нас внезапно возникла отрицательная частота. На первый взгляд кажется, что отрицательные частоты — это какая-то глупость. В самом деле, что такое −1 Гц? Однако эта концепция не сложнее, чем отрицательные вещественные числа в целом.

Никто никогда не видел −2 яблока или −100 рублей, но в наши дни отрицательные числа мало кого тревожат. Между прочим, так было далеко не всегда. Физический смысл −100 рублей зависит от контекста. Он может означать, что мы взяли денег взаймы, или что за ноль была принята какая-то другая точка отсчета. Например, нулем считается себестоимость товара. Тогда знак минус говорит о том, что товар был продан ниже себестоимости, то есть, убыточно.

Так же и с отрицательными частотами. В примере с квадратурным смесителем у нас есть частота гетеродина, которую можно принять за ноль. Тогда все, что ниже по спектру, становится отрицательными частотами, а все что выше — положительными частотами. Чтобы окончательно в этом убедиться, предлагаю вам посмотреть на график со спиралью и подумать, что будет, если заменить f на −f. Вспоминаем, что косинус является четной функцией, а синус — нечетной. То есть, cos(−x) = cos(x), sin(−x) = −sin(x).

Но при этом в преобразовании Фурье отрицательные частоты несут иной смысл. Синус и косинус определены как для положительных, так и для отрицательных аргументов. Когда мы раскладываем функцию на частотные составляющие, у нас нет объективных причин считать, что в ней есть cos(+ωt), но нет cos(−ωt), или наоборот. Поэтому мы получаем отклик как на положительных, так и на отрицательных частотах.

Напоследок хочется подчеркнуть, что синфазный и квадратурный сигналы — это один сигнал. Просто мы хотим иметь в этом сигнале чуть больше информации, чем зависимость амплитуды от времени. По этой причине и возникает лишнее измерение, а привычные синусы и косинусы становятся спиралями.

Дополнение: В продолжение темы см посты Шпаргалка по работе DSP фильтров и Рассчитываем DSP фильтры при помощи SciPy.

Метки: SDR, Беспроводная связь.