Основы создания 3D-моделей в OpenSCAD
3 мая 2025
Рано или поздно перед любым 3D-печатником встает вопрос о выборе программы для 3D-моделирования. Таких программ немало, в том числе и бесплатных. Для технических моделей есть FreeCAD и OpenSCAD, а для художественных — Blender. В свое время я попробовал все из перечисленного и остановился на OpenSCAD, как наиболее подходящем для моих задач. Давайте же разберемся, как пользоваться OpenSCAD, на примере конкретной модели.
Если открыть сайт OpenSCAD и зайти на страницу Downloads, то вам предложат скачать OpenSCAD версии 2021.01. Может сложиться впечатление, что проект заброшен. Однако ниже на той же странице в разделе Development Snapshots доступна версия 2025.05.02. Версия для разработчиков работает лучше.
Создание моделей в OpenSCAD происходит при помощи текстового описания. Для меня, как программиста, это очень удобно и привычно. Также это отлично работает с системами контроля версий.
Интерфейс программы поделен на две части. Слева пишем код, справа смотрим на то, что получается. Если вам не нравится текстовый редактор в OpenSCAD, можно его закрыть, и открыть вместо него окно с Vim, Sublime Text, или в чем вам удобно программировать.
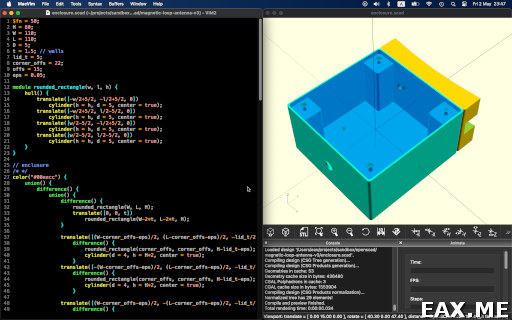
Я обычно закрываю редактор OpenSCAD и открываю MacVim (кликабельно):
На скриншоте показан корпус для магнитной рамочной антенны.
Итак, давайте же нарисуем что-нибудь в OpenSCAD. Что-то не сложное, но в то же время иллюстрирующее наиболее важные примитивы. Поискав по своим старым проектам, я нашел стакан для ручек. Не самая захватывающая модель, но для обучения сгодится.
Давайте подумаем, что такое стакан для ручек? В первом приближении это «вытянутый куб», или, говоря более строго — прямоугольный параллелепипед.
Так и запишем:
S = 80; // ширина
cube([S, S, H], center = true);
В окне справа видим:
Чтобы получился стакан, из этого параллелепипеда нужно как бы «вырезать» еще один параллелепипед. У математиков это называется вычитанием:
H = 89;
S = 80;
T = 6;
difference() {
/* уменьшаемое */
cube([S, S, H], center = true);
/* вычитаемое */
translate([0,0,T/2+eps])
cube([S-2*T, S-2*T, H-T], center = true);
}
Переменная T — это толщина всех стенок стакана. Вычитаемый параллелепипед меньше уменьшаемого по высоте на T. Центры обоих фигур находятся в начале координат. Чтобы получился стакан, мы переносим вычитаемое вверх по оси Z на T/2+esp, где eps — это произвольная небольшая величина. Подробности о том, зачем нужна eps, описаны в документации на difference.
Начинает быть похоже на стакан:
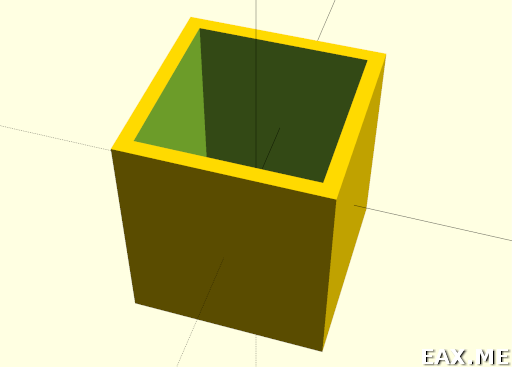
Только мне не нравятся острые углы. Хотелось бы их скруглить.
В подобных случаях на помощь приходит сумма Минковского:
R = 3;
H = 95-2*R;
S = 80;
T = 6-2*R+eps;
$fn = 30;
minkowski() {
/* эта часть без изменений */
difference() {
cube([S, S, H], center = true);
translate([0,0,T/2+eps])
cube([S-2*T, S-2*T, H-T], center = true);
}
sphere(r = R);
}
Сумму Минковского можно объяснить на пальцах таким образом. Представьте, что у вас есть куб и шар. Берем шар и перемещаем его центр по всем точкам, принадлежащим кубу. Множество точек, хотя бы раз попавших в шар в ходе его перемещений, и есть сумма Минковского двух фигур. Мне нравится думать об этом, как о «помазать шаром по кубу».
Из новых переменных здесь введена R — это радиус шара. Чтобы стакан не стал толще после minkowski(), H и T были уменьшены на величину 2*R. Специальная переменная $fn задает уровень детализации шара. Слишком большой ее делать не стоит, иначе понадобится много ресурсов на отрисовку.
Полученный результат:
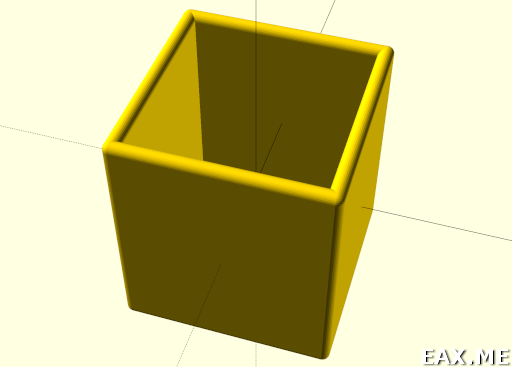
Здесь мне не нравится, что дно стакана тоже получилось скругленным. Это не обязательно такая уж большая проблема. Однако в 3D-печати лучше не делать лишних нависаний, если можно их не делать.
Нарисуем дно стакана, каким мы хотим его получить:
translate([S/2,S/2,-(H+R+eps)/2])
#cylinder(r = R, h = R, center = true);
translate([S/2,-S/2,-(H+R+eps)/2])
#cylinder(r = R, h = R, center = true);
translate([-S/2,S/2,-(H+R+eps)/2])
#cylinder(r = R, h = R, center = true);
translate([-S/2,-S/2,-(H+R+eps)/2])
#cylinder(r = R, h = R, center = true);
}
Вот что мы увидим в итоге:
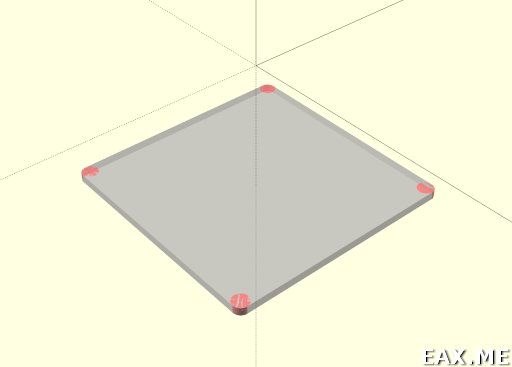
Когда вы пишите # рядом с определением фигуры, она подсвечивается красным. Если же написать %, фигура становится полупрозрачной. Удобно для отладки.
Итак, имеется четыре цилиндра радиусом R и такой же высоты. Высота здесь не очень важна. Значение, ранее присвоенное переменной $fn, влияет также и на детализацию цилиндров. Цилиндры разнесены по четырем углам. Затем к цилиндрам применяется трансформатор hull, создающий выпуклую оболочку. Мне нравится думать об этом, как о «натянуть резину на цилиндры».
Осталось лишь объединить нарисованный ранее стакан с его новым основанием:
R = 3;
H = 95-2*R;
S = 80;
T = 6-2*R+eps;
$fn = 30;
/* объединение; работает как объединение множеств из точек */
union() {
/* полностью скругленный стакан */
minkowski() {
difference() {
cube([S, S, H], center = true);
translate([0,0,T/2+eps])
cube([S-2*T, S-2*T, H-T], center = true);
}
sphere(r = R);
}
/* его новое основание без нависаний */
hull() {
translate([S/2,S/2,-(H+R+eps)/2])
cylinder(r = R, h = R, center = true);
translate([S/2,-S/2,-(H+R+eps)/2])
cylinder(r = R, h = R, center = true);
translate([-S/2,S/2,-(H+R+eps)/2])
cylinder(r = R, h = R, center = true);
translate([-S/2,-S/2,-(H+R+eps)/2])
cylinder(r = R, h = R, center = true);
}
}
Модель готова. Однако сейчас мы находимся в режиме предпросмотра. Чтобы окончательно отрендерить модель, нажимаем F6. Затем для экспорта в формат STL нажимаем F7.
Отправляем модель на печать, и вот он окончательный результат:
Заметьте, что модель сразу получилась параметрической. Например, чтобы сделать стакан выше, достаточно поменять одну переменную в коде.
Само собой разумеется, рассмотреть абсолютно все возможности OpenSCAD в рамках одного поста не представляется возможным. В качестве источников дополнительной информации рекомендую онлайн-шпаргалку по OpenSCAD, а также книгу Programming with OpenSCAD.
Метки: 3D печать.
Вы можете прислать свой комментарий мне на почту, или воспользоваться комментариями в Telegram-группе.