Памятка по работе кучи и пирамидальной сортировки
26 июня 2025
Многие программисты могут по памяти реализовать односвязные и двусвязные списки, хэш-таблицы или алгоритм быстрой сортировки. Это классика алгоритмов и структур данных, которая к тому же часто используется на практике. Но если вдруг понадобится написать кучу или реализовать пирамидальную сортировку, то, не знаю как вы, а я по памяти вряд ли смогу это сделать. Давайте же освежим знания в этой области. А чтобы думалось непосредственно об алгоритмах, а не об управлении памятью, писать будем на Python.
Куча — это структура данных, часто используемая для реализации очередей с приоритетами. Основными операциями над кучей являются вставка и извлечение элемента. Извлечение происходит в соответствии с порядком (приоритетом) элементов. Если первыми извлекаются элементы с меньшим значением ключа, говорят, что это min-куча, а если с большим, то max-куча. Существует с десяток разных вариантов кучи. В рамках этого поста мы рассмотрим лишь традиционную двоичную кучу (пирамиду). Вставка и извлечение в ней происходят за O(log(N)).
Без потери общности рассмотрим пример max-кучи. Логически она представляет собой двоичное дерево:
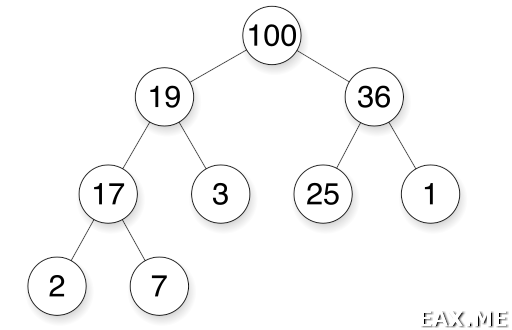
В этом дереве всегда выполняются два условия. Во-первых, дочерние элементы меньше родителей. Таким образом, в корне дерева всегда находится элемент с максимальным значением. Min-куча работает наоборот. Во-вторых, последний уровень дерева заполняется слева направо без пропусков. Говорят, что двоичное дерево является полным (complete). Как следствие, глубина двух листьев может отличаться не более чем на единицу.
Физически двоичная куча хранится в массиве:
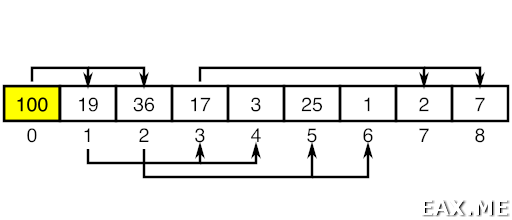
Для любого i-го элемента массива элемент с номером (i - 1) // 2 является предком, а элементы 2*i + 1 и 2*i + 2 — потомками. Таким образом, не нужно лишней памяти для хранения указателей в дереве. Примечательно, что любой отсортированный по убыванию массив является корректной max-кучей.
Принимая во внимание написанное выше, не сложно догадаться, как в двоичной куче работают вставка и извлечение элементов. При вставке мы помещаем новый элемент в конец массива, после чего тот «всплывает» к корню до тех пор, пока не будут восстановлены свойства кучи. Аналогично, при извлечении мы помещаем последний элемент массива на место корня, после чего тот «тонет» к листьям до восстановления свойств кучи. В английском языке вместо «всплывать» и «тонуть» принята терминология «просеивать вверх / вниз» (sift up / down, не путать с shift).
То же самое в переводе на Python:
# size - размер кучи на момент вызова (+= 1 после вызова)
def heap_insert(arr, size, x):
if size >= len(arr):
raise IndexError("Cannot insert into a full heap")
arr[size] = x
_sift_up(arr, size, size + 1)
def _sift_up(arr, idx, size):
if idx == 0:
return
parent = (idx - 1) // 2
if arr[idx] > arr[parent]:
arr[idx], arr[parent] = arr[parent], arr[idx]
_sift_up(arr, parent, size)
# arr - преаллоцированный массив фиксированного размера
# size - размер кучи на момент вызова (-= 1 после вызова)
def heap_extract(arr, size):
if size == 0:
return None
max_element = arr[0]
if size > 1:
arr[0] = arr[size - 1]
_sift_down(arr, 0, size - 1)
return max_element
def _sift_down(arr, idx, size):
largest = idx
left = 2 * idx + 1
right = 2 * idx + 2
if left < size and arr[left] > arr[largest]:
largest = left
if right < size and arr[right] > arr[largest]:
largest = right
if largest != idx:
arr[idx], arr[largest] = arr[largest], arr[idx]
_sift_down(arr, largest, size)
Пирамида может быть использована для сортировки массивов без использования дополнительной памяти (in-place). Это называется пирамидальной сортировкой. Алгоритм состоит из двух этапов.
Этап первый. Массив преобразуется в max-кучу. Проще всего это сделать так. Берем первый элемент массива и считаем его кучей из одного элемента. Берем второй элемент. Теперь первые два элемента массива выделены под кучу. Из них второй пока что не используется. Добавлыем элемент в кучу. Получили кучу из двух элементов. Продолжаем для оставшихся элементов массива. В результате получаем кучу, содержащую все элементы массива. Данный алгоритм имеет асимптотическую сложность O(N*log(N)). Есть и более эффективный алгоритм, который мы рассмотрим далее.
Этап второй. Есть max-куча. Извлекаем из нее один элемент. Помещаем его на освободившееся место в конце массива. Повторяем для всех элементов. Получили массив, отсортированный по возрастанию. Данный этап также имеет сложность O(N*log(N)). Итого, весь алгоритм имеет сложность O(N*log(N)).
Первый этап можно оптимизировать. Сразу считаем весь массив кучей. Идем по предпоследнему уровню кучи. «Топим» текущий узел в соответствии с обычной логикой. Повторяем для всех узлов уровня. Затем для уровня выше. Повторяем до самого корня.
Более строго, в переводе на Python:
def _heapify(arr):
n = len(arr)
for i in range(n // 2 - 1, -1, -1):
_sift_down(arr, i, n)
Хоть это и не так очевидно, можно показать, что алгоритм имеет асимптотическую сложность O(N). Итоговая сложность алгоритма сортировки остается O(N*log(N)), но на практике она будет работать быстрее.
Окончательная реализация пирамидальной сортировки получается такой:
_heapify(arr)
for i in range(len(arr) - 1, 0, -1):
arr[0], arr[i] = arr[i], arr[0]
_sift_down(arr, 0, i)
Пирамидальная сортировка примечательна тем, что обладает асимптотической сложностью O(N*log(N)) во всех случаях — наихудшем, наилучшем и среднем. Быстрая сортировка имеет O(N^2) в худшем случае. Тем не менее, на практике быстрая сортировка оказывается быстрее. Чтобы избежать наихудшего сценария достаточно выбирать опорный элемент случайным образом.
Поэтому пирамидальная сортировка используется редко. Еще один недостаток данного алгоритма заключается в том, что его не так-то просто распараллелить. Быстрая сортировка распараллеливается вполне естественным образом.
Напоследок отмечу, что в стандартной библиотеке языка Python есть пакет heapq, который реализует очередь с приоритетом описанным выше образом. Если вы пишите на C, то готовую реализацию пирамиды можно взять из исходного кода PostgreSQL. Соответствующий файл называется binaryheap.c. Что же до полной версии исходников к данному посту, то она доступна здесь.
Вы можете прислать свой комментарий мне на почту, или воспользоваться комментариями в Telegram-группе.