Учимся работать с текстурами в Haskell'евом OpenGL
В прошлый раз мы научились рисовать разноцветные треугольники и пирамиды. Это, конечно, замечательно, но если вы когда-нибудь играли в компьютерные игры, то знаете, что они рисуют на экране очень, очень много пикселей самых разных цветов. Неужели все их приходится раскрашивать вручную при помощи изученных в прошлой заметке средств? К счастью, нет. Для решения этой проблемы были придуманы текстуры.
Текстуры в OpenGL бывают одномерные, двумерные и трехмерные. Чаще всего приходится иметь дело с двумерными текстурами. Можно думать о таких текстурах, как о картинках, ширина и высота которых являются степенями двойки. Точка определенного цвета на текстуре называется тексел (от texture element). Например, текстура 64x64 состоит из 4096 текселей. В памяти компьютера текстура может хранится в различных форматах, например, RGB8, RGBA8 или R3G3B2. В первом случае один тексел занимает три байта, во второй – четыре, в третьем – один байт. На жестком диске текстуры хранятся в обычных графических форматах, таких как bmp, jpg или png.
Вспомним, как рисуется цветной треугольник. Мы указываем координаты вершин треугольника в трехмерном пространстве и указываем цвет каждой вершины. Если все вершины имеют красный цвет, треугольник будет красным. Если цвета разные, внутренние точки треугольника будут иметь усредненный цвет в зависимости от расстояния этих точек до каждой из вершин. При использовании текстур идея аналогичная, только вместо цвета вершин указываются координаты на текстуре. При рисовании примитива мы как бы вырезаем часть текстуры и натягиваем ее на рисуемый примитив. В итоге точки примитива оказываются раскрашены в цвета, взятые из текстуры.
Рассмотрим небольшой вспомогательный модуль для рисования текстурированных четырехугольников:
module Utils.Drawing where
import Graphics.Rendering.OpenGL
data TexturedQuad = TexturedQuad
{ _rx1, _ry1, _rz1
, _rx2, _ry2, _rz2
, _rx3, _ry3, _rz3
, _rx4, _ry4, _rz4
, _tx1, _tx2, _ty1, _ty2 :: GLfloat
}
drawTexturedQuad :: TexturedQuad -> IO ()
drawTexturedQuad (TexturedQuad x1 y1 z1 x2 y2 z2
x3 y3 z3 x4 y4 z4
tx1 tx2 ty1 ty2) = do
renderPrimitive Quads $ do
texCoord $ TexCoord2 tx1 ty1
vertex $ Vertex3 x1 y1 z1
texCoord $ TexCoord2 tx1 ty2
vertex $ Vertex3 x2 y2 z2
texCoord $ TexCoord2 tx2 ty2
vertex $ Vertex3 x3 y3 z3
texCoord $ TexCoord2 tx2 ty1
vertex $ Vertex3 x4 y4 z4
Здесь четырехугольник задается координатами четырех точек в трехмерном пространстве, а также координатами двух точек на двумерной текстуре. Перед указанием координаты каждой из вершин четырехугольника вызовом функции vertex также происходит указание координаты соответствующей точки на текстуре при помощи функции texCoord. Заметьте, что при рисовании четырехугольника все четыре его вершины должны лежать в одной плоскости. Иначе при просмотре под определенным углом четырехугольник может быть прорисован неверно. При работе с треугольниками у нас не возникало такой проблемы, потому что три точки всегда лежат в одной плоскости. Также при рисовании любого примитива в наших интересах, чтобы примитив не был вырожденным.
Рассмотрим программу, рисующую три кирпичные стены:
import Graphics.Rendering.OpenGL
import Graphics.UI.GLUT
import Graphics.GLUtil (readTexture)
import Control.Monad (forM_)
import Utils.Drawing (TexturedQuad(..), drawTexturedQuad)
main = do
_ <- getArgsAndInitialize
_ <- createWindow "Textured Walls"
initialDisplayMode $= [WithDepthBuffer, DoubleBuffered]
depthFunc $= Just Less
texture Texture2D $= Enabled
setupGeometry
Right tex <- readTexture "./data/bricks.png"
displayCallback $= display tex
mainLoop
setupGeometry :: IO ()
setupGeometry = do
matrixMode $= Projection
perspective 50.0 1.0 0.3 10.0
matrixMode $= Modelview 0
translate $ Vector3 0.0 0.0 (-3.0 :: GLfloat)
display :: TextureObject -> IO ()
display tex = do
clear [ColorBuffer, DepthBuffer]
drawWalls tex
swapBuffers
drawWalls :: TextureObject -> IO ()
drawWalls tex = do
textureBinding Texture2D $= Just tex
textureFilter Texture2D $= ((Linear', Nothing), Linear')
textureFunction $= Replace
forM_ [leftWall, frontWall, rightWall] drawTexturedQuad
leftWall =
let (x1, x2, y1, y2, z1, z2) = (-0.9, -0.9, -0.6, 0.6, 0.6, -1.0)
(tx1, tx2, ty1, ty2) = (3, 0, 1, 0) in
wallTemplate x1 x2 y1 y2 z1 z2 tx1 tx2 ty1 ty2
frontWall =
let (x1, x2, y1, y2, z1, z2) = (0.8, -0.8, -0.6, 0.6, -1.0, -1.0)
(tx1, tx2, ty1, ty2) = (3, 0, 4, 0) in
wallTemplate x1 x2 y1 y2 z1 z2 tx1 tx2 ty1 ty2
rightWall =
let (x1, x2, y1, y2, z1, z2) = (0.9, 0.9, -0.6, 0.6, 0.6, -1.0)
(tx1, tx2, ty1, ty2) = (0.9, 0.1, 0.9, 0.1) in
wallTemplate x1 x2 y1 y2 z1 z2 tx1 tx2 ty1 ty2
wallTemplate x1 x2 y1 y2 z1 z2 tx1 tx2 ty1 ty2 =
TexturedQuad x1 y1 z1 x1 y2 z1 x2 y2 z2 x2 y1 z2 tx1 tx2 ty1 ty2
Здесь мы впервые используем двойную буферизацию. В initialDisplayMode для этого указывается флаг DoubleBuffered, а вместо используемой ранее функции flush вызывается swapBuffers. Впрочем, в контексте данной заметки разница между использованием одного и двух буферов совершенно незаметна.
Строкой texture Texture2D $= Enabled мы включаем поддержку двумерных текстур. Далее используется очень полезная функция readTexture из пакета GLUtil. Она загружает текстуры из многих графических форматов, избавляя нас от необходимости самостоятельно декодировать их. Но следует быть начеку. Например, пакет JuicyPixels, используемый в GLUtil, не поддерживает так называемый «Progressive JPEG». Поэтому, если вы хотите уменьшить размер текстуры, сохранив ее в формате JPEG с помощью Gimp, не забудьте снять соответствующую галочку.
Много нового для нас происходит в функции setupGeometry. В OpenGL такие преобразования, как переносы, масштабирования и вращения, осуществляются при помощи матриц. Вспомним, как мы вращали основание пирамиды в прошлой заметке:
rotateXZ an (x, y, z) =
let x' = (x * cos an) - (z * sin an)
z' = (x * sin an) + (z * cos an)
in (x', y, z')
Это же преобразование можно представить в виде матрицы, а поворот вершины – умножением матрицы поворота на вектор координат этой вершины. То же самое относится и к другим преобразованиям. (Так вот, оказывается, для чего нужна линейная алгебра!)
Строкой matrixMode $= Projection мы говорим, что хотим что-то сделать с матрицей проекций. По умолчанию в OpenGL используется ортогональное проецирование. При его использовании два одинаковых объекта, находящихся на разном расстоянии от нас, выглядят одинаково большими. Это не совсем то, к чему мы привыкли в реальной жизни, не так ли? Вызовом perspective 50.0 1.0 0.3 10.0 мы переключаемся на более привычное перспективное проецирование. Если при ортогональном проецировании объем видимости представляет собой прямоугольный параллелепипед, то в случае перспективного проецирования используется симметричная усеченная пирамида. Аргументы функции perspective называются fovy, aspect, near и far. Следующая картинка хорошо объясняет, что они задают:
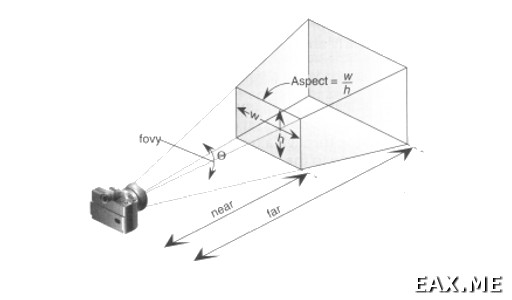
Затем мы выбираем модельно-видовую матрицу (matrixMode $= Modelview 0). Следующий далее вызов функции translate смещает объекты на сцене на -3 единицы по оси Z. Или перемещает камеру на +3 единицы. Это как посмотреть. Дело в том, что для модельных (то есть, изменения сцены) и видовых преобразований (перемещения камеры) OpenGL использует один набор функций и одну матрицу. Так или иначе, принимая во внимание, что по умолчанию камера находится в точке (0,0,0) и смотрит вниз по оси Z, если теперь мы нарисуем что-то в начале координат, оно будет находится перед камерой на расстоянии 3 единицы.
В функции drawWalls мы выбираем текстуру, которую хотим использовать. Код textureFilter Texture2D $= ((Linear', Nothing), Linear') означает, что когда для закраски примитива текстуру приходится сжать или растянуть, будет использован средневзвешенный цвет по массиву текселей 2x2. Наконец, textureFunction $= Replace говорит, что при раскраске примитива цвет пикселя нужно заменить на цвет, указанный в текстуре. Помимо замещения есть и другие режимы. Например, можно смешивать текстуру с цветом примитива, тем самым придавая текстуре различные оттенки.
В результате получается такая картинка:

Немного психоделично, да? В действительности, вы видите три абсолютно одинаковые по размеру стены, расположенные буквой «П». Что между ними разного – это координаты точек на текстуре. Для правой стены текстура бралась из прямоугольника 0.1 ≤ X ≤ 0.9, 0.1 ≤ Y ≤ 0.9. В результате у текстуры были немного обрезаны края, а то, что осталось, было натянуто на стену. Для левой стены был взят прямоугольник 0 ≤ X ≤ 3, 0 ≤ Y ≤ 1. Текстура всегда имеет размер 1x1 единиц, а при выходе за ее пределы изображение копируется. На левой стене вы видите три копии текстуры, расположенные горизонтально. Наконец, на стене, расположенной к нам лицом, использовался прямоугольник 0 ≤ X ≤ 3, 0 ≤ Y ≤ 4, поэтому на нем вы видите 12 экземпляров одной и той же текстуры.
Рассмотрим еще одну программу, рисующую деревянный ящик:
import Graphics.Rendering.OpenGL
import Graphics.UI.GLUT
import Graphics.GLUtil (readTexture)
import Control.Monad (forM_)
import Utils.Drawing (TexturedQuad(..), drawTexturedQuad)
main = do
_ <- getArgsAndInitialize
_ <- createWindow "Textured Box"
initialDisplayMode $= [WithDepthBuffer, DoubleBuffered]
depthFunc $= Just Less
texture Texture2D $= Enabled
setupGeometry
Right tex <- readTexture "./data/box.jpg"
displayCallback $= display tex
mainLoop
setupGeometry :: IO ()
setupGeometry = do
matrixMode $= Projection
perspective 40.0 1.0 1.0 10.0
matrixMode $= Modelview 0
translate $ Vector3 0 0 (-5 :: GLfloat)
rotate 30 $ Vector3 1 0 ( 0 :: GLfloat)
rotate (-30) $ Vector3 0 1 ( 0 :: GLfloat)
display :: TextureObject -> IO ()
display tex = do
clear [ColorBuffer, DepthBuffer]
drawBox tex
swapBuffers
drawBox :: TextureObject -> IO ()
drawBox tex = do
textureBinding Texture2D $= Just tex
textureFilter Texture2D $= ((Linear', Nothing), Linear')
textureFunction $= Replace
forM_ [boxFront, boxBack, boxTop, boxBottom, boxLeft, boxRight]
drawTexturedQuad
boxFront = faceTemplate ( 1, -1, 1, -1, 1, 1)
boxBack = faceTemplate ( 1, -1, 1, -1, -1, -1)
boxLeft = faceTemplate (-1, -1, 1, -1, 1, -1)
boxRight = faceTemplate ( 1, 1, 1, -1, 1, -1)
boxTop = faceTemplateXZ ( 1, -1, 1, 1, -1)
boxBottom = faceTemplateXZ ( 1, -1, -1, 1, -1)
faceTemplate (x1, x2, y1, y2, z1, z2) =
TexturedQuad x1 y1 z1 x1 y2 z1 x2 y2 z2 x2 y1 z2 0 1 0 1
faceTemplateXZ (x1, x2, y, z1, z2) =
TexturedQuad x1 y z1 x1 y z2 x2 y z2 x2 y z1 0 1 0 1
Из новых функций мы здесь видим только rotate. Она поворачивает камеру против часовой стрелки на указанное количество градусов вокруг луча из начала координат, проходящего через заданную точку. Здесь мы поворачиваем камеру на 30 градусов вокруг оси X, а потом на 30 градусов вокруг оси Y. В результате камера смотрит на ящик немного сверху и справа:

Как видите, работать с текстурами в OpenGL не особо сложно. Конечно, за кадром осталось еще много вопросов, в том числе мультитекстурирование, MIP mapping и множество других интересных вещей. Но о них как-нибудь в другой раз.
Все исходники к заметке вы найдете в этом архиве.
Дополнение: Простой кроссплатформенный OpenGL-проект на C++