Аппроксимация функции с помощью сплайна Безье
18 октября 2010
Представьте себе такую задачу. Есть N точек на плоскости. Требуется провести в непосредственной близости от них гладкую кривую. Точки эти могут представлять собой экспериментальные данные на графике или координаты, по которым пользователь кликнул мышкой в графическом редакторе. Так вот, одно из решений этой задачи заключается в использовании кривых Безье.
Кривая Безье для N точек задается полином степени (N−1). Вот как выглядит этот полином для для N = 4:
B(t) = (1 − t)3P0 + 3 t (1 − t)2P1 + 3 t2(1 − t) P2 + t3P3, t ∈ [0;1]
Здесь Pi — это наши точки, t — параметр функции, меняя значение которого в диапазоне от 0 до 1, можно получить координаты всех точек кривой Безье. Общий вид функции для произвольного числа точек и очень красивую иллюстрацию к ней можно посмотреть в Википедии.
Приведенную формулу несложно проверить в Excel или OpenOffice:
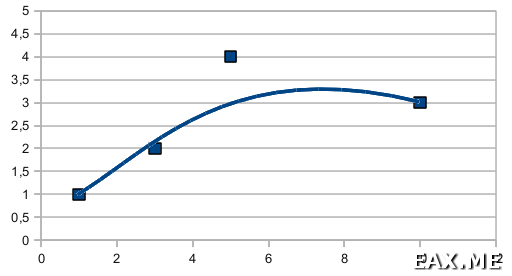
Хорошо, с четырьмя точками понятно. А что делать, если точек 10 или 10 000? Кривую Безье можно построить для любого числа точек, но вычислять полиномы десятитысячной степени — это мягко говоря грустно. Делают очень просто — разбивают точки на группы по 4 штуки, строят для каждой из них кривую Безье и соединяют полученные сегменты в одну кривую.
Единственная проблема — полученная кривая будет «не очень гладкой» на границах сегментов. Спрашивается — что делать? И снова все оказывается очень просто (хотя ответ в сети хрен найдешь). Допустим, у нас есть шесть точек. Пусть (x3; y3) и (x4; y4) — координаты третьей и четвертой точки соответственно. Вставляем между ними дополнительную точку с координатами x’ = (x3 + x4)/2 и y’ = (y3 + y4)/2, после чего проводим одну кривую через точки 1-4, а вторую — через точки 4-7.
В результате получим одну гладкую кривую для шести точек. Если учесть поведение кривой Безье и то, что точки (x3; y3), (x’; y’) и (x4; y4) лежат на одной прямой, это становится вполне очевидно. Собственно полученная кривая и есть сплайн. Если точек больше шести, их нужно разбить по схеме 3-2-2…2-2-3 и связать полученные группы с помощью дополнительных точек, как описано выше. Последнюю точку можно повторить несколько раз, если множество точек не делится на целое число групп.
Сплайны Безье нашли широкое применение. Например, они используются в шрифтах TrueType и графическом редакторе GIMP. Вообще сплайны — довольно полезная вещь.
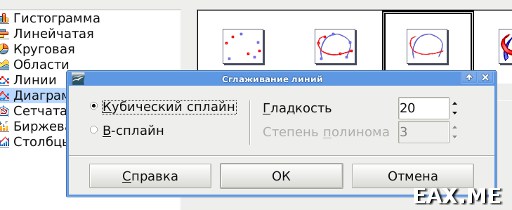
Кубический сплайн полностью разжеван в Википедии. В отличие от сплайна Безье он интерполирует функцию по нескольким известным точкам, то есть, точно проходит через каждую из них. B-сплайн — это более общий случай сплайна Безье.
Здесь вы можете скачать демонстрационный пример к заметке. Для просмотра документа понадобится OpenOffice.
Дополнение: В продолжение темы — Генетические алгоритмы на практике.
Метки: Алгоритмы.
Вы можете прислать свой комментарий мне на почту, или воспользоваться комментариями в Telegram-группе.