Записки программиста

Чтобы честно вычислить значение медианы для множества каких-то значений, необходимо взять эти значения, сложить в массив, отсортировать его, после чего взять средний элемент массива. Аналогично вычисляются и прочие процентили. Если значений много, то процесс выходит долгим и/или может не хватить памяти. Поэтому есть интерес к алгоритмам, вычисляющим приблизительные значения процентилей. Рассмотрим некоторые из них.

Проще всего посчитать процентили, если что-то заранее известно о природе данных. Допустим, что наши значения — это время ответа веб-сервера. Тогда можно быть довольно уверенным, что значения лежат где-то в интервале от 1 мс до 30 000 мс. В этом случае просто создаем 30 000 счетчиков и сводим задачу к сортировке подсчетом. Если время ответа действительно измеряется с точностью до миллисекунды, и оно ограничено 30 секундами, то мы получим не приблизительные значения, а самые что ни на есть истинные.

Может быть такое, что уникальных значений много, а память ограничена. Тогда данные можно распределять по «корзинам». В сценарии с временем ответа веб-сервера возьмем все данные и целочисленно поделим их, к примеру, на 8. Уникальных значений стало намного меньше, в результате чего задача свелась к предыдущей. Ответ мы получим с точностью до 8 мс. Во многих случаях данной точности хватает за глаза.

Однако что делать, если мы вообще ничего не знаем о данных?

Простейшее решение заключается в том, чтобы взять резервуарную выборку от значений, после чего вычислить процентили не от всех значений, а от резервуара. Но насколько точными будет результат?

Для получения ответа на этот вопрос был написан небольшой скрипт на Python. Код скрипта ничем не примечателен, поэтому подробно разбирать его не будем. Заинтересованные читатели могут изучить скрипт самостоятельно. Если вы не знакомы с Matplotlib, обратите внимание на заметку Построение диаграмм на Python с помощью Matplotlib.

Были получены такие графики:

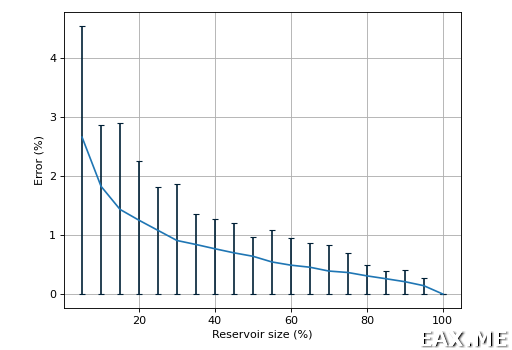
Скрипт вычисляет медиану от 100 000 целочисленных значений, равномерно распределенных в интервале от 0 до 4999. По оси OX — размер резервуара в процентах от объема исходных данных. По оси OY — ошибка вычисления медианы в процентах относительно истинного значения. Черные столбики показывают разброс между минимальной и максимальной ошибкой в ходе тысячи экспериментов. Синий график — это 95-ый процентиль ошибки.

Вместо равномерного распределения можно взять и логнормальное:

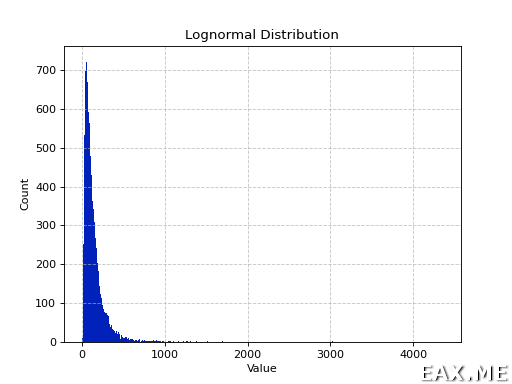
Данная гистограмма построена при помощи отдельного скрипта. Логнормальное распределение куда лучше эмитирует ситуацию с временем ответа веб-сервера. У последнего обычно имеется «длинный хвост», что может сказаться на точности алгоритма вычисления процентилей.

Если построить аналогичный график для логнормального распределения, то он получится практически идентичным приведенному выше. Разница проявляется, если считать не медиану, а 95-ый процентиль.

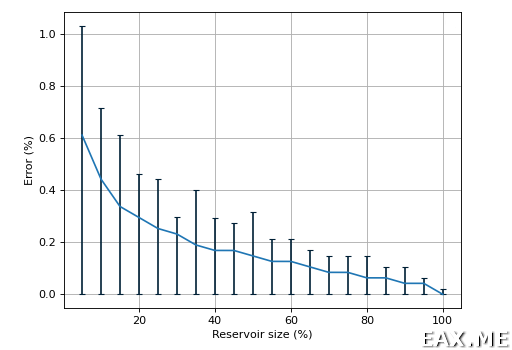
Для равномерного распределения:

Для логнормального:

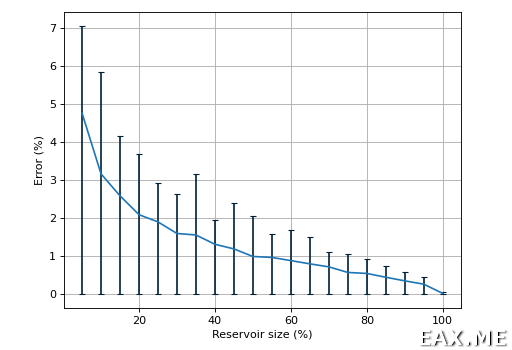
При прочих равных ошибка для логнормального распределения выше.

Спрашивается, насколько маленьким может быть резервуар? Путем аналогичных экспериментов приходим к выводу, что не стоит делать резервуар меньше 2% от размера исходных данных. Иначе ошибка значения 95-го процентиля для случая логнормального распределения сильно превышает 10%. Еще большая ошибка на практике скорее всего недопустима.

Перечисленные решения являются простыми, понятными, и позволяют выбирать между объемом используемой памяти и точностью результата. Если же они по какой-то причине не подходят, то можно рассмотреть альтернативные подходы. В качестве последних можно назвать алгоритмы UDDSketch и T-Digest.

Дополнение: В комментариях Kright верно отметил, что для вычисления одного заданного процентиля не требуется сортировать массив целиком, как я написал в первом абзаце. Базовая идея — как в алгоритме quicksort, только на очередном шаге рекурсии мы отбрасываем неинтересующую нас часть массива. Алгоритм называется quickselect. Используя удачные эвристики при выборе опорного элемента можно получить алгоритм с асимптотической сложностью O(n) — см introselect и median of medians.

Метки: Python, Алгоритмы.