Записки программиста

Аудио-фильтры на пассивных компонентах в наши дни используют редко. RC-фильтры не могут обеспечить крутизны АЧХ больше 6 дБ на октаву. Этого недостатка лишены LC-фильтры. Однако на частотах 0-20 кГц им требуются катушки индуктивности на десятки-сотни миллигенри. Такие катушки делают, но они сравнительно дороги, а выбор номиналов ограничен. Поэтому обычно используют активные фильтры, речь о которых и пойдет далее.

Теория: простые фильтры

Активные фильтры, как несложно догадаться, используют активные компоненты. Обычно это операционные усилители. Для примера рассмотрим простой фильтр нижних частот. Его можно сделать, добавив конденсатор в обычную неинвертирующую схему включения операционного усилителя:

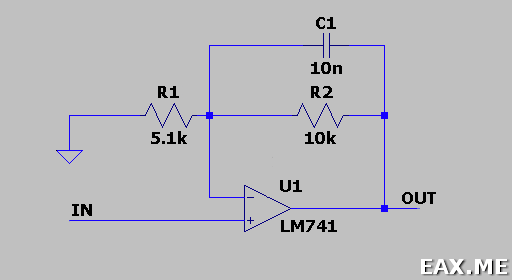
Без C1 схема просто увеличивает амплитуду сигнала в 1 + R2 / R1 раз, что в нашем случае соответствует:

… примерно 9.5 дБ. На низких частотах C1 ничего не делает, и схема работает как обычно. Но чем выше частота, тем большая часть сигнала обходит R2 через C1, и тем меньше усиление. Получаем ни что иное, как фильтр нижних частот.

Рассчитаем АЧХ этого фильтра с помощью LTspice:

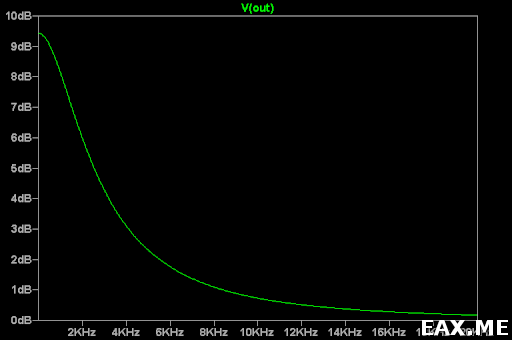
Аналогично можно сделать фильтр высоких частот, соединив конденсатор параллельно с R1. Фильтры на основе инвертирующей схемы включения ОУ делаются по тому же принципу. Но инвертирующая схема неудобна тем, что имеет низкий входной импеданс, а неинвертирующая схема имеет минимальное усиление 0 дБ. Не во всех задачах нужно, чтобы фильтр усиливал сигнал.

Теория: топология Саллена-Ки

Поэтому были придуманы другие топологии активных фильтров. О них хорошо рассказано в статье об активных фильтрах на Википедии и далее по ссылкам. Мы рассмотрим лишь самую популярную, топологию Саллена-Ки (Sallen–Key topology).

Так выглядит схема фильтра нижних частот:

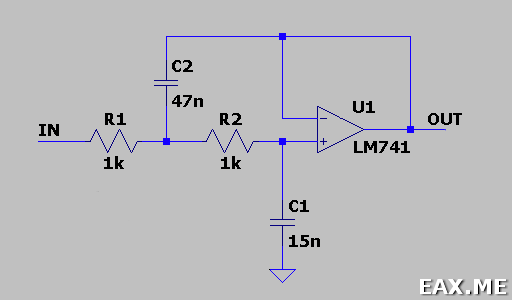
На низких частотах C1 и C2 имеют высокий импеданс. В результате схема превращается в повторитель напряжения (буфер). С ростом частоты импеданс C1 падает, и все меньшая часть сигнала попадает на неинвертирующий вход операционного усилителя. Как следствие, падает уровень выходного сигнала. Теперь C2 почти что подключен к земле. В итоге схема работает, как два последовательно соединенных RC-фильтра, и достигает крутизны АЧХ в 12 дБ на октаву.

А почему бы просто не использовать два RC-фильтра? Так иногда делают, но у этого подхода есть проблема. Первый RC-фильтр в цепочке видит второй фильтр, как нагрузку, соединенную параллельно с конденсатором. Поэтому второй фильтр должен иметь высокий импеданс, а его нагрузка — еще более высокий. Активные фильтры не накладывают таких ограничений.

Вернемся к нашему фильтру. Его частота среза приходится:

… приблизительно на 6 кГц:

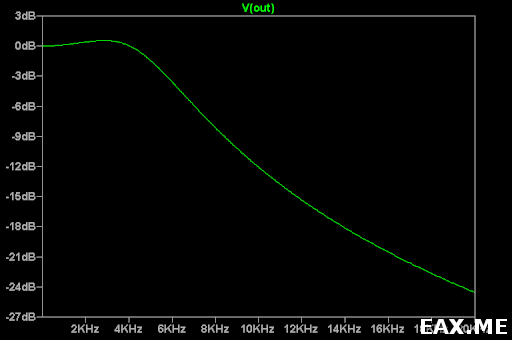
Можно заметить, что на некоторых частотах в полосе пропускания фильтр имеет небольшое усиление. Насколько будет гладкой АЧХ в полосе пропускания определяется величиной Q. Она также вычисляется из R1, R2, C1 и C2:

Чем больше Q, тем больше пик при переходе от полосы пропускания к полосе подавления.

Топология и принцип работы фильтра высоких частот аналогичны, только R и C меняются местами:

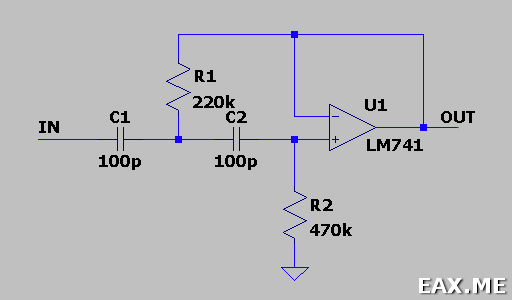
Частота среза определяется по той же формуле:

Q вычисляется немного иначе:

Фильтр обладает следующей АЧХ:

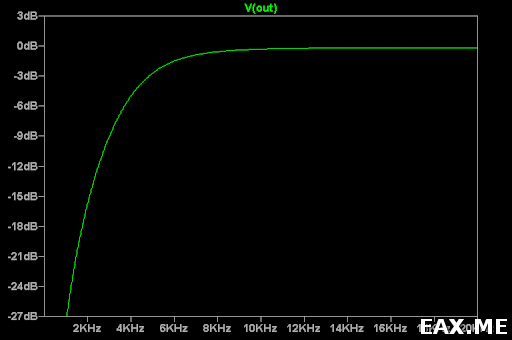
Q получился меньше, чем в прошлый раз. Теперь никакого усиления в полосе пропускания не наблюдается.

Практика

Все три приведенных фильтра были спаяны на макетной печатной плате:

Здесь использованы операционные усилители LM741 (даташит [PDF]). Выбор ОУ не принципиален. LM741 можно заменить на TL081. Он менее шумный (Vn = 18 nV/√Hz против 28 nV/√Hz), имеет большую частоту единичного усиления (3 МГц против 1.5 МГц), может работать при меньшем напряжении питания, а также стоит дешевле. LM741 и TL081 имеют одинаковую распиновку. Существуют аналогичные чипы TL082 и TL084. Они содержат два и четыре ОУ в одном корпусе соответственно. Ранее использованные нами NE5532 и LM358 тоже подойдут.

Если раньше вы не использовали LM741, у вас может возникнуть вопрос, к чему подключать выходы offset null, пины 1 и 5. В приведенных схемах, да и в целом при работе с AC-сигналами, эти пины не используются и ни к чему не подключаются. Они нужны при работе с DC-сигналами, и то не во всех схемах. Дело в том, что при равности напряжений на инвертирующем и неинвертирующем входах выход ОУ должен быть нулевым. Но поскольку транзисторы в ОУ не идеальны, это свойство нарушается. LM741 можно подстроить, включив потенциометр между пинами 1 и 5.

Фильтры были проверены при помощи осциллографа Rigol DS1054Z и генератора сигналов MHS-5200A. Их поведение соответствует моделям с точностью до погрешности в номиналах компонентов.

Заключение

Само собой разумеется, все варианты активных фильтров в рамках одного поста рассмотреть невозможно. При проектировании нового фильтра помогают LTspice, а также различные калькуляторы фильтров. Например, есть онлайн-калькулятор от компании Analog Devices. Также калькулятор активных фильтров есть в открытом приложении Qucs. Читателям, которые хотят больше углубиться в теорию, можно порекомендовать книгу Op Amp Applications Handbook.

Все модели, использованные в статье, вы найдете в этом архиве.

Дополнение: Измеренная АЧХ фильтра нижних частот приводится в обзоре генератора сигналов и частотомера Rigol DG4162. Еще примеры фильтров вы найдете в статьях Активный фильтр для приема телеграфа и Активный телеграфный фильтр HI-PER-MITE.

Дополнение: Больше схем активных фильтров, включая схемы полосовых и режекторных фильтров, приводится в видео Active RC-filter Basics на канале FesZ Electronics.

Метки: Аудио, Электроника.