Записки программиста

Сегодня я хотел бы начать публикацию серии заметок про эту животрепещущую тему, по которой недавно вышла моя новая книга, а именно введение в понимание квантовой вычислительной модели. Я благодарю моего доброго товарища и коллегу Александра за предоставленную возможность размещения в его блоге гостевых постов на эту тему.

Я постарался сделать эту кратчайшую заметку как можно более простой с точки зрения понимания неподготовленным читателем, который, однако, хотел бы понять, что такое квантовые вычисления. Тем не менее, от читателя требуется владеть базовым пониманием информатики. Ну и общее математическое образование тоже не помещало бы :). В статье нет формул, всё объясняется словами. Тем не менее, все вы можете задавать мне вопросы в комментариях, и я постараюсь объяснять, как только могу.

Что такое квантовые вычисления?

Начнём с того, что квантовые вычисления — это новая очень модная тема, которая там у них развивается семимильными шагами по нескольким направлениям (а у нас, как всякая фундаментальная наука пребывает в запустении и отдана на откуп нескольким учёным, сидящим в своих башнях из слоновой кости). И вот уже говорят о появлении первых квантовых компьютеров (D-Wave, но это не универсальный квантовый компьютер), ежегодно публикуются новые квантовые алгоритмы, создаются языки квантового программирования, сумрачный гений Международных Деловых Машин в тайных подземных лабораториях производит квантовые вычисления на десятках кубитов.

Что же это такое? Квантовые вычисления — это вычислительная модель, которая отличается от модели Тьюринга и фон Неймана, и предполагается, что для некоторых задач она является более эффективной. По крайней мере найдены задачи, для которых модель квантовых вычислений даёт полиномиальную сложность, в то время как для классической вычислительной модели неизвестно алгоритмов, которые имели бы сложность, ниже экспоненциальной (но, с другой стороны, пока ещё не доказано, что таких алгоритмов не существует).

Как такое может быть? Всё просто. Квантовая вычислительная модель основана на нескольких довольно простых правилах преобразования входной информации, которые обеспечивают массовую параллелизацию вычислительных процессов. Другими словами, можно одновременно вычислить значение функции для всех её аргументов (и это будет единственный вызов функции). Это достигается специальной подготовкой входных параметров и специальным же видом функции.

Светитель Проц учит, что всё это суть синтаксическая манипуляция с математическими символами, за которой, по сути, нет никакого смысла. Есть формальная система с правилами преобразования входа в выход, и эта система позволяет при помощи последовательного применения этих правил получать из входных данных выходные. Всё это в конечном итоге сводится к перемножению матрицы и вектора. Да, да, да. Вся модель квантовых вычислений основана на одной простой операции — умножении матрицы на вектор, в результате чего на выходе получается другой вектор.

Светитель Халикаарн в противоположность учит, что существует объективный физический процесс, который выполняет указанную операцию, и только лишь существование которого и обуславливает возможность массовой параллелизации вычислений функции. То, что мы воспринимаем это как умножение матрицы на вектор, является всего лишь способом нашего далеко не совершенного отражения объективной реальности в нашем разуме.

Мы в нашей научной лаборатории имени светителей Проца и Халикаарна объединяем эти два подхода и говорим, что модель квантовых вычислений есть математическая абстракция, которая отражает объективный процесс. В частности, числа в векторах и матрицах являются комплексными, хотя это совершенно не увеличивает вычислительную мощность модели (она бы была такой же мощной и с действительными числами), однако выбраны именно комплексные числа потому, что найден объективный физический процесс, который осуществляет такие преобразования, как описывает модель, и в котором используются именно комплексные числа. Этот процесс называется унитарной эволюцией квантовой системы.

В основе квантовой вычислительной модели лежит понятие кубита. Это практически то же самое, что и бит в классической теории информации, однако кубит может одновременно принимать несколько значений. Говорят, что кубит находится в суперпозиции своих состояний, то есть значение кубита есть линейная комбинация его базовых состояний, и коэффициенты при базовых состояниях как раз являются комплексными числами. Базовыми же состояниями являются известные по классической теории информации значения 0 и 1 (в квантовых вычислениях их принято обозначать |0> и |1>).

Пока не очень-то и понятно, в чём фишка. А фишка вот в чём. Суперпозиция одного кубита записывается как A|0> + B|1>, где A и B — некоторые комплексные числа, единственное ограничение на которые заключается в том, что сумма квадратов их модулей всегда должна равняться 1. А если рассмотреть два кубита? Два бита могут получать 4 возможных значения: 00, 01, 10 и 11. Резонно предположить, что два кубита представляют собой суперпозицию четырёх базовых значений: A|00> + B|01> + C|10> + D|11>. И так оно и есть. Три кубита представляют собой суперпозицию восьми базовых значений. Другими словами, квантовый регистр из N кубитов одновременно хранит в себе 2N комплексных чисел. Ну а с математической точки зрения это есть 2N-мерный вектор в комплекснозначном пространстве. Именно этим достигается экспоненциальная мощность модели квантовых вычислений.

Далее функция, которая применяется к входным данным. Поскольку теперь входные данные представляют собой суперпозицию всех возможных значений входного аргумента, функция должна быть преобразована в такой вид, чтобы принять такую суперпозицию и обработать её. Тут тоже всё более или менее просто. В рамках модели квантовых вычислений каждая функция представляет собой матрицу, на которую накладывается одно ограничение — она должна быть эрмитовой. Это значит, что при умножении этой матрицы на свою эрмитово-сопряжённую, должна получиться единичная матрица. Эрмитово-сопряжённая матрица получается при помощи транспонирования исходной матрицы и заменой всех её элементов на их комплексно-сопряжённые. Это ограничение следует из упомянутого ранее ограничения на квантовый регистр. Дело в том, что если такую матрицу умножить на вектор квантового регистра, то в результате получится новый квантовый регистр, сумма квадратов модулей комплекснозначных коэффициентов при квантовых состояниях которого всегда равна 1.

Показано, что любую функцию можно специальным образом преобразовать в такую матрицу. Также показано. что любую эрмитову матрицу можно выразить посредством тензорного произведения небольшого набора базисных матриц, представляющих базисные логические операции. Тут всё примерно так же, как в классической вычислительной модели. Эта более сложная тема, которая выходит за рамки данной обзорной статьи. То есть сейчас главное понять — любая функция может быть выражена в виде матрицы, подходящей для использования в рамках модели квантовых вычислений.

Что происходит дальше? Вот у нас есть входной вектор, который представляет собой суперпозицию различных вариантов значений входного параметра функции. Есть функция в виде эрмитовой матрицы. Квантовый алгоритм представляет собой умножение матрицы на вектор. В результате получается новый вектор. Что же это за ерунда-то такая?

Дело в том, что в модели квантовых вычислений есть ещё одна операция, которая называется измерением. Мы можем измерить вектор и получить из него конкретное значение кубита. То есть суперпозиция схлопывается в конкретное значение. И вероятность получения того или иного значения равна квадрату модуля комплекснозначного коэффициента. И теперь понятно, почему сумма квадратов должна равняться 1, поскольку при измерении всегда будет получено какое-то конкретное значение, а потому сумма вероятностей их получения равна единице.

То есть что получается? Имея N кубитов можно одновременно обработать 2N комплексных чисел. И в выходном векторе будут результаты обработки всех этих чисел одновременно. В этом мощь модели квантовых вычислений. Но получить можно только одно значение, и оно может быть каждый раз различное в зависимости от распределения вероятностей. В этом ограничение модели квантовых вычислений.

Суть квантового алгоритма заключается в следующем. Создаётся равновероятностная суперпозиция всех возможных значений входного параметра. Эта суперпозиция подаётся на вход функции. Далее по результатам её выполнения делается вывод о свойствах этой функции. Дело в том, что мы не можем получить все результаты, но вот сделать выводы о свойствах функции можем вполне. И в следующем разделе будут показаны несколько примеров.

Пара интересных квантовых алгоритмов

В подавляющем большинстве источников по квантовым вычислениям читатель найдёт описания нескольких алгоритмов, которые, собственно, обычно используются для демонстрации мощи вычислительной модели. Здесь мы тоже кратко и поверхностно рассмотрим такие алгоритмы (два из них, которые демонстрируют различные базовые принципы квантовых вычислений). Ну а для детального ознакомления с ними опять адресую к своей новой книге.

Алгоритм Дойча

Это первый алгоритм, который был разработан для того, чтобы показать суть и эффективность квантовых вычислений. Задача, которую решает этот алгоритм, совсем оторвана от реальности, однако на ней как раз можно показать базовый принцип, положенный в основу модели.

Итак, пусть есть некоторая функция, которая получает на вход один бит и возвращает на выходе тоже один бит. Честно говоря, таких функций может быть всего 4. Две из них являются константными, то есть одна всегда возвращает 0, а другая всегда возвращает 1. Две другие являются сбалансированными, то есть возвращают 0 и 1 в равных количествах случаев. Вопрос: как за один вызов этой функции определить, константная она или сбалансированная?

Очевидно, что в классической вычислительной модели этого сделать нельзя. Необходимо дважды вызвать функцию и сравнить результаты. А вот в модели квантовых вычислений это сделать можно, поскольку функция будет вызвана только один раз. Посмотрим…

Как уже было написано, мы подготовим равновероятностную суперпозицию всех возможных значений входного параметра функции. Поскольку на входе у нас один кубит, то его равновероятностная суперпозиция готовится при помощи одного применения гейта Адамара (это такая специальная функция, которая и готовит равновероятностные суперпозиции :). Далее снова применяется гейт Адамара, который работает таким образом, что если ему на вход подаётся равновероятностная суперпозиция, то он преобразует её назад в состояния |0> или |1> в зависимости от того, в какой фазе находится равновероятностная суперпозиция. После этого производится измерение кубита, и если он равен |0>, то рассматриваемая функция константна, а если |1>, то сбалансирована.

Что получается? Как уже было сказано, при измерении мы не можем получить все значения функции. Но мы можем сделать определённые выводы о её свойствах. Задача Дойча как раз и спрашивает о свойстве функции. И это свойство очень простое. Ведь как выходит? Если функция константна, то сложение по модулю 2 всех её выходных значений всегда даёт 0. Если же функция сбалансирована, то сложение по модулю 2 всех её выходных значений всегда даёт 1. Именно этот результат мы и получили в результате выполнения алгоритма Дойча. Мы не знаем, какое именно значение вернула функция на равновероятностной суперпозиции всех входных значений. Мы знаем только, что это тоже суперпозиция результатов, и если теперь эту суперпозицию преобразовать специальным образом, то будут сделаны однозначные выводы о свойстве функции.

Вот как-то так.

Алгоритм Гровера

Другой алгоритм, который показывает квадратичный выигрыш по сравнению с классической вычислительной моделью, решает более приближённую к реальности задачу. Это алгоритм Гровера, или, как называет его сам Лов Гровер, алгоритм поиска иголки в стоге сена. Этот алгоритм основан на другом принципе, лежащем в основе квантовых вычислений, а именно амплификации.

Уже упоминалась некая фаза, которая может быть у квантового состояния в составе кубита. Как таковой фазы нет в классической модели, это что-то новенькое именно в рамках квантовых вычислений. Фазу можно понимать как знак у коэффициента при квантовом состоянии в суперпозиции. Алгоритм Гровера основан на том, что специально подготовленная функция меняет фазу у состояния |1>.

Алгоритм Гровера решает обратную задачу. Если есть неупорядоченый набор данных, в котором надо найти один элемент, удовлетворяющий критерию поиска, алгоритм Гровера поможет это сделать эффективнее, чем простой перебор. Если простой перебор решает задачу за O(N) обращений к функции, то алгоритм Гровера эффективно находит заданный элемент за O(√N) обращений к функции.

Алгоритм Гровера состоит из следующих шагов:

1. Инициализация начального состояния. Опять готовится равновероятностная суперпозиция всех входных кубитов.

2. Применение итерации Гровера. Данная итерация состоит из последовательного применения функции поиска (она определяет критерий поиска элемента) и специального гейта диффузии. Гейт диффузии меняет коэффициенты при квантовых состояниях, вращая их вокруг среднего. Тем самым производится амплификация, то есть увеличение амплитуды искомого значения. Фишка в том, что осуществить применение итерации необходимо определённое количество раз (√2n), иначе алгоритм вернёт не те результаты.

3. Измерение. После измерения входного квантового регистра с большой вероятностью будет получен искомый результат. Если необходимо увеличить достоверность ответа, то алгоритм прогоняется несколько раз и вычисляется совокупная вероятность правильного ответа.

Интерес в данном алгоритме представляет то, что он позволяет решить произвольную задачу (например, любую из класса NP-полных), предоставляя пусть и не экспоненциальное, но существенное повышение эффективности по сравнению с классической вычислительной моделью. В одной из будущих статей будет показано, как это можно сделать.

Квантовый зоопарк

Тем не менее, уже нельзя говорить о том, что учёные продолжают сидеть в своей башне из слоновой кости. Несмотря на то, что многие квантовые алгоритмы разрабатываются для каких-то странных и непонятных матаноподобных задач (например, определение порядка идеала конечного кольца), уже разработан ряд квантовых алгоритмов, которые решают очень даже прикладные задачи. В первую очередь это задачи из области криптографии (компрометация различных криптографических систем и протоколов). Далее идут типовые математические задачи на графах и матрицах, при этом такие задачи имеют очень большую область применения. Ну и есть ряд алгоритмов аппроксимации и эмуляции, которые используют аналоговую составляющую модели квантовых вычислений.

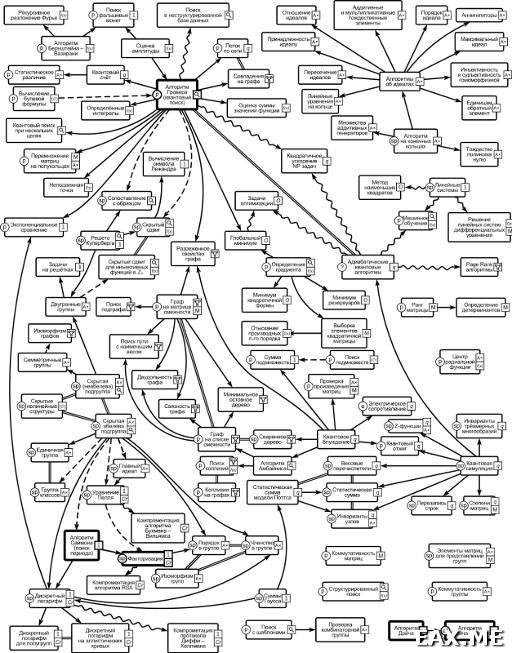
В сети Интернет по адресу http://math.nist.gov/quantum/zoo/ ведётся полный список квантовых алгоритмов. Его версия, актуальная на 05.09.2011, в переведённом виде имеется в уже неоднократно упомянутой моей книге. Здесь нет смысла перечислять все эти многочисленные алгоритмы, которых уже более 50. Приведём лишь диаграмму отношений квантовых алгоритмов и задач (кликабельно, 871 Кб):

На представленной диаграмме прямоугольником обозначается квантовый алгоритм или задача, которая может быть решена в рамках модели квантовых вычислений. Для каждого алгоритма и задачи приводятся две характеристики — ускорение и типы задач, решаемых алгоритмом (или тип самой задачи). Наконец, между алгоритмами и (или) задачами рассматриваются четыре типа отношений, а именно:

• Если из алгоритма A идёт обычная стрелка в алгоритм B, то это значит, что алгоритм B основан на алгоритме A.
• Если же стрелка пунктирная, то алгоритм B сводится к алгоритму A, то есть это в большей мере отношение подобия.
• Волнистая стрелка обозначает, что алгоритм A решает прикладную задачу B.
• Наконец, двойная линия между прямоугольниками без стрелок обозначает, что два алгоритма сходны между собой.

Заключение

В заключение хотелось бы ещё раз поблагодарить хозяина этого блога, а также сообщить, что всё, что написано в этой краткой заметке, более подробно (и даже в некоторых местах использованы математические формулы довольно жуткого вида) написано у меня в книге «Квантовые вычисления и функциональное программирование», которую всякий желающий может свободно скачать и прочитать.

Я буду рад получить комментарии и замечания. Ваши вопросы задавайте здесь или присылайте мне на почту. Постараюсь на всё ответить и всё разъяснить. Дерзайте!

Дополнение: Алгоритм Шора, его реализация на языке Haskell и результаты некоторых опытов

Метки: Алгоритмы, Параллелизм и многопоточность.