Решение задачи про игру «кошки-мышки» на OCaml
13 февраля 2013
В прошлые выходные прошел очередной конкурс по функциональному программированию от Darkus’а. Поразмыслив, я решил принять в нем участие с целью немного попрактиковаться в изучаемом мною эзотерическом и никому не нужном языке программирования OCaml. В результате занял четвертое место.
Условия задачи были следующие. Есть коробка из пяти последовательно соединенных друг с другом ячеек. Внутри находится мышка, снаружи — кошка. Кошка не видит, что происходит в коробке, но она может опускать свою лапу в одну из пяти ячеек. Если в ячейке находится мышка, грызун отправляется на обед. В противном случае мышка случайным образом перемещается в одну из соседних ячеек (которых либо две, либо одна, если мышка находится в одной из крайних ячеек). Затем кошке дается еще одна попытка. Нужно определить кратчайшую последовательность ходов для кошки, которая гарантировано приводит к поимке мышки. В какой ячейке находится мышка изначально — неизвестно.
Посидев немного с ручкой и бумажкой, я нарисовал примерно такую картинку:
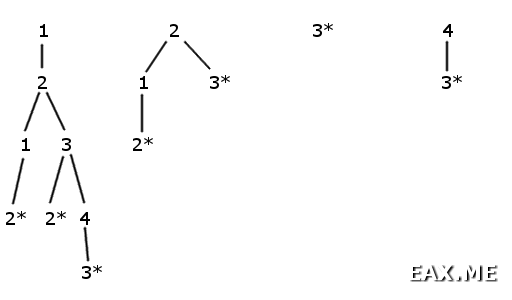
Для простоты здесь рассматривается аналогичная задача с четырьмя ячейками. Цифрами обозначается номер ячейки, в котором может находится мышка на текущем шаге. Первой строке сверху соответствует первый шаг игры, второй — второй шаг, и так далее. Дугами показаны возможные переходы мышки из одной ячейки в другую. Звездочками обозначаются ходы кошки. На приведенной картинке кошка совершает последовательность ходов 3-3-2-2-3. Легко видеть, что данная последовательность ведет к гарантированной поимке мышки.
Имея перед глазами такую наглядную иллюстрацию, совсем несложно написать алгоритм решения задачи с произвольным числом ячеек:
let start_moves_list box_size =
[? List: [x] | x <- 1 -- box_size ?]
let next_moves_list box_size moves_list =
List.concat (
List.map
(fun lst -> [? List: x :: lst | x <- 1 -- box_size ?] )
moves_list
)
let rec catched node box_size moves =
match node, box_size, moves with
| _, _, [] -> false
| node, box_size, move :: other_moves ->
if node > box_size ||
node <= 0 ||
node == move then true
else
catched (node-1) box_size other_moves &&
catched (node+1) box_size other_moves
let is_solution box_size moves =
List.fold_left
(fun acc x -> acc && catched x box_size moves)
true
[? List: x | x <- 1 -- box_size ?]
let rec find_solutions' box_size moves_list =
match List.filter
(is_solution box_size)
moves_list with
| [] -> find_solutions' box_size
(next_moves_list box_size moves_list)
| solutions -> solutions
let find_solutions box_size =
find_solutions' box_size (start_moves_list box_size)
С помощью функции start_moves_list мы генерируем все возможные последовательности шагов единичной длины. Проверяем, является ли одна из этих последовательностей решением задачи. За это отвечает функция is_solution. Если решение или решения найдены, возвращаем результат. В противном случае генерируем все возможные последовательности шагов на единицу длиннее и возвращаемся к этапу проверки.
Последовательность шагов является решением задачи, если она приводит к поимке мыши независимо от номера ячейки, в котором она находилась изначально (функция is_solution). Последовательность шагов приводит к поимке мыши в ячейке node, если (а) шаг кошки из головы списка шагов приходится как раз на эту ячейку или если (б) шаги кошки из хвоста списка приводят к поимке мыши независимо от того, переместится ли она в ячейку node-1 или node+1 (функция catched).
Задача с пятью ячейками имеет целых четыре решения: 4-3-2-4-3-2, 2-3-4-4-3-2, 4-3-2-2-3-4 и 2-3-4-2-3-4. У задачи с четырьмя ячейками только два решения — 2-3-3-2 и 3-2-2-3. Во как! Оказывается, в этом случае задачу можно решить всего лишь за четыре шага, а не за пять. Совершенно очевидно, что описанный выше алгоритм всегда находит кратчайшие последовательности шагов. Не менее очевидно, что если A-B-C-…-Z является решением задачи, то и Z-…-C-B-A также является решением, так как задача симметрична и мы можем нумеровать ячейки как слева направо, так и справа налево.
На этапе проверки предлагалось решить ту же задачу для ста ячеек. Однако приведенный алгоритм плохо работает уже для семи ячеек. По понятным причинам. Спрашивается, что делать?
Если внимательно присмотреться к задаче, можно обратить внимание на две вещи. Во-первых, среди решений для N ячеек всегда найдется одно, имеющее вид 2-3-…-(N-1)-(N-1)-(N-2)-…-2:
let lst = [? List: x | x <- 2 -- (n-1) ?]
in List.concat [lst; List.rev lst]
Во-вторых, проверку, является ли последовательность ходов решением задачи, можно существенно ускорить:
let next_moves set box_size =
IntSet.fold
(fun n acc ->
let acc' = if n-1 > 0 then IntSet.add (n-1) acc else acc
in if n+1 <= box_size then IntSet.add (n+1) acc' else acc')
set (IntSet.empty)
let rec is_solution set lst box_size =
if IntSet.is_empty set then true
else match lst with
| [] -> false
| hd :: tl ->
let set' = next_moves (IntSet.remove hd set) box_size
in is_solution set' tl box_size
let check_solution sol n =
is_solution [? IntSet: x | x <- 1 -- n ?] sol n
Проверяем:
- : bool = true
Осталось всего лишь доказать, что для случая с сотней ячеек не существует более коротких решений. Совершенно очевидно, что проверять перебором мы это будем очень долго. Тут я умываю руки, поскольку математик из меня никчемный. Если вы любите математические задачи, и для вас это раз плюнуть, я бы с удовольствием ознакомился с вашим доказательством. Надеюсь, я в нем хоть что-нибудь смогу понять. Также можете попробовать доказать, то gen_solution всегда генерирует самое короткое решение для любого числа ячеек N.
Дополнение: Почему я все-таки упарываюсь Haskell’ем, а не OCaml’ом
Метки: OCaml, Функциональное программирование.
Вы можете прислать свой комментарий мне на почту, или воспользоваться комментариями в Telegram-группе.