Примеры использования Python-библиотеки NumPy
Я много слышал про библиотеку NumPy, что дескать в ней есть много полезных математических функций, или что-то в этом роде. Однако какой-то практической задачи, где был бы нужен NumPy, мне как-то не подворачивалось, и потому большого интереса изучать данную библиотеку у меня не было. Потом я заинтересовался Software Defined Radio, и, как следствие, цифровой обработкой сигналов. И вот тут иногда возникает желание по-быстрому поиграться в REPL, скажем, с быстрым преобразованием Фурье (Fast Fourier Transform, FFT) или чем-то таким. Оказалось, что это задача как раз для NumPy. Поэтому было решено разобраться в возможностях этой библиотеки как следует, выяснив заодно, что в ней еще есть помимо FFT.
Простой пример: как выглядит функция?
Для начала попробуем понять общую идею, стоящую за NumPy. Главным объектом, которым оперирует NumPy, является массив. Например, следующий код объявляет массив целых чисел от -5 до 5:
>>> import numpy as np
>>> x = np.linspace(-5, 5, 11)
>>> x
array([-5., -4., -3., -2., -1., 0., 1., 2., 3., 4., 5.])
Массивы не обязательно должны быть именно одномерными, но пока что остановимся на одномерных. Массивы можно складывать, вычитать и умножать:
>>> x - x
array([0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.])
>>> x * x
array([25., 16., 9., 4., 1., 0., 1., 4., 9., 16., 25.])
Также определены арифметические операции между массивами и числами:
>>> 10 + 2 * x
array([ 0., 2., 4., 6., 8., 10., 12., 14., 16., 18., 20.])
А еще массивы имеют разные полезные методы, например:
>>> (x / 2).round()
array([-2., -2., -2., -1., -0., 0., 0., 1., 2., 2., 2.])
Само собой разумеется, массивы NumPy можно преобразовывать в обычные списки языка Python, и обратно:
>>> y = np.array([1,2,3])
>>> y
array([1, 2, 3])
>>> y.tolist()
[1, 2, 3]
Вы спросите, а в чем практическая польза таких массивов? Допустим, мы хотим по-быстрому посмотреть, как выглядит график какой-то функции. Для определенности возьмем сигмоиду, часто используемую в качестве функции активации в нейронных сетях. Рисовать будем при помощи уже знакомой нам библиотеки Matplotlib.
С NumPy код получается крайне простым:
import matplotlib.pyplot as plt
import numpy as np
x = np.linspace(-5, 5, 100)
def sigmoid(alpha):
return 1 / ( 1 + np.exp(- alpha * x) )
dpi = 80
fig = plt.figure(dpi = dpi, figsize = (512 / dpi, 384 / dpi) )
plt.plot(x, sigmoid(0.5), 'ro-')
plt.plot(x, sigmoid(1.0), 'go-')
plt.plot(x, sigmoid(2.0), 'bo-')
plt.legend(['A = 0.5', 'A = 1.0', 'A = 2.0'], loc = 'upper left')
fig.savefig('sigmoid.png')
Результат:
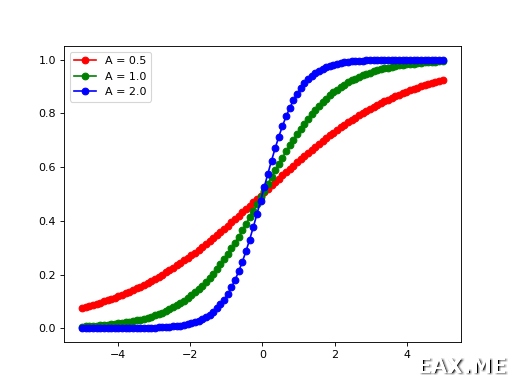
Заметьте, что больше не нужно писать циклы, вычисляющие значение функции в различных точках, поскольку NumPy делает все это за нас. Фактически, мы просто применяем функции к функциям и выводим получившиеся функции. Декларативное и чисто функциональное программирование в самом натуральном его виде!
Всякая статистика
Иногда бывает нужно по-быстрому посчитать медиану или, скажем, 99-ый процентиль по каким-то значениям. NumPy приходит на помощь и здесь.
Сгенерим немного случайных данных:
>>> import numpy as np
>>> ones = np.ones(50)
>>> rnd = np.random.random(50) * 0.1
>>> samples = ones + rnd
Посчитаем среднее:
>>> np.average(samples)
1.0456167098847502
>>> np.mean(samples)
1.0456167098847502
Медиану:
>>> np.median(samples)
1.0446054794173638
Процентили:
>>> np.percentile(samples, 50)
1.0446054794173638
>>> np.percentile(samples, 95)
1.0957859973475361
>>> np.percentile(samples, 99)
1.0973855545421
Максимум, минимум, peak-to-peak:
>>> samples.max()
1.0967179044332522
>>> samples.min()
1.0060578855891802
>>> samples.ptp()
0.09066001884407204
А заодно уж и стандартное отклонение с дисперсией:
>>> np.std(samples)
0.027949661469244255
>>> np.var(samples)
0.000781183576245357
Использованная выше функция np.random.random генерирует случайные числа с равномерным распределением. А если мы хотели бы использовать нормальное распределение? Нет проблем:
>>> import matplotlib.pyplot as plt
>>> samples = np.random.normal(loc=0, scale=5, size=100000)
>>> plt.hist(samples, 200)
>>> plt.show()
Помимо нормального и равномерного распределения NumPy также предлагает beta, dirichlet, gamma, binomial, exponential, и другие.
Линейная алгебра
До сих пор мы рассматривали одномерные массивы. Когда массив двумерный, он фактически становится матрицей. А там где матрицы, там и линейная алгебра.
Объявим несколько матриц:
>>> import numpy.matlib
>>> import numpy.linalg
>>> m1 = np.arange(1, 10).reshape(3,3)
>>> m1
array([[1, 2, 3],
[4, 5, 6],
[7, 8, 9]])
>>> m2 = np.identity(3)
>>> m2
array([[1., 0., 0.],
[0., 1., 0.],
[0., 0., 1.]])
Транспонируем первую матрицу, а также посчитаем след и детерминант второй:
>>> m1.transpose()
array([[1, 4, 7],
[2, 5, 8],
[3, 6, 9]])
>>> m2.trace()
3.0
>>> np.linalg.det(m2)
1.0
Матрицы можно складывать, умножать на число, умножать на вектор, а также умножать на другую матрицу:
>>> m1 + m2
array([[ 2., 2., 3.],
[ 4., 6., 6.],
[ 7., 8., 10.]])
>>> m1 * 3
array([[ 3, 6, 9],
[12, 15, 18],
[21, 24, 27]])
>>> m1 + np.array([1,2,3])
array([[ 2, 4, 6],
[ 5, 7, 9],
[ 8, 10, 12]])
>>> m1 * m2
array([[1., 0., 0.],
[0., 5., 0.],
[0., 0., 9.]])
Посчитать матрицу, обратную к данной, можно функцией np.linalg.inv:
>>> m3 = np.matlib.rand(3, 3)
>>> (m3 * np.linalg.inv(m3))
matrix([[1.0000000e+00, 0.0000000e+00, 0.0000000e+00],
[0.0000000e+00, 1.0000000e+00, 0.0000000e+00],
[4.4408921e-16, 0.0000000e+00, 1.0000000e+00]])
>>> (m3 * np.linalg.inv(m3)).round()
matrix([[1., 0., 0.],
[0., 1., 0.],
[0., 0., 1.]])
На первый взгляд, линейная алгебра может показаться не самым интересным предметом. Но это только до тех пор, пока вы не попытаетесь писать свои игровой движок на OpenGL. Кое-какие подробности по этой теме можно найти в посте Продолжаем изучение OpenGL: управление камерой при помощи мыши и клавиатуры.
FFT и обратный FFT
Казалось бы, в начале поста была сказано про FFT, а в итоге вместо FFT мы говорим про какие-то там массивы и матрицы. Ладно, пожалуйста, вот вам FFT:
#!/usr/bin/env python3
import numpy as np
import matplotlib.pyplot as plt
dpi = 80
tau = 2 * np.pi
t = np.linspace(0, 0.5, 500)
x_1 = 0.9 * np.sin(100 * tau * t)
x_2 = 0.4 * np.sin(150 * tau * t)
x = x_1 + x_2
N = x.size
# x = x * np.hamming(N)
fig = plt.figure(dpi = dpi, figsize = (512 / dpi, 384 / dpi) )
plt.plot(t, x)
plt.xlabel("Time (s)")
plt.ylabel("Amplitude")
fig.savefig("x.png")
plt.close()
X = np.fft.fft(x)
# t[1] - t[0] = sample rate
# 1/(t[1] - t[0]) = frequency
freq = np.linspace(0, 1 / (t[1] - t[0]), N)[: (N // 2)]
# 1 / N is a normalization factor
X_amp = (1/N) * np.abs(X)[: (N // 2)]
X_phs = (1/N) * np.angle(X)[: (N // 2)]
fig = plt.figure(dpi = dpi, figsize = (512 / dpi, 384 / dpi) )
plt.bar(freq, X_amp)
plt.xlabel("Frequency (Hz)")
plt.ylabel("Amplitude")
fig.savefig("X_amp.png")
plt.close()
fig = plt.figure(dpi = dpi, figsize = (512 / dpi, 384 / dpi) )
plt.bar(freq, X_phs)
plt.xlabel("Frequency (Hz)")
plt.ylabel("Amplitude")
fig.savefig("X_phs.png")
plt.close()
fig = plt.figure(dpi = dpi, figsize = (512 / dpi, 384 / dpi) )
x2 = np.fft.ifft(X)
plt.plot(t, x2.real)
plt.ylabel("Amplitude")
plt.xlabel("Time (s)")
fig.savefig("x2.png")
plt.close()
Исходный сигнал:
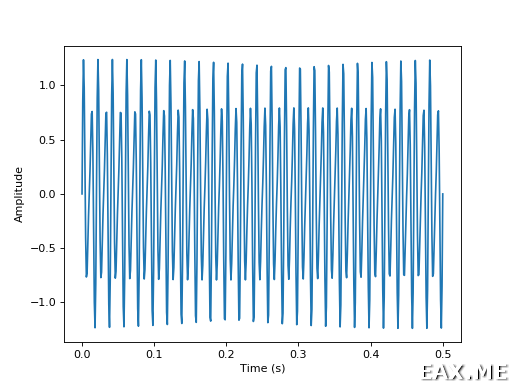
Его разложение на частоты:
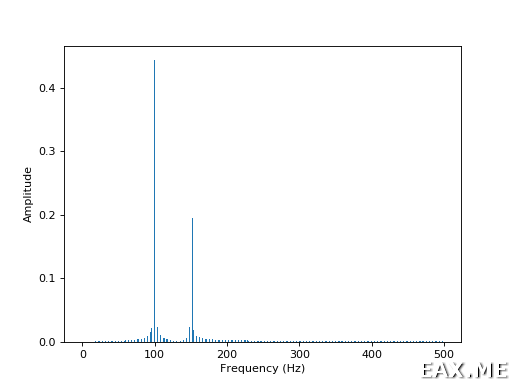
К сожалению, объяснение преобразования Фурье выходит за рамки данного поста. Однако по этой теме есть масса источников в интернете. В частности, можно порекомендовать статью Understanding the Fourier Transform by example в блоге ritchievink.com. Приведенный выше отрывок кода основан на коде из этой статьи.
Заключение
Как видите, библиотека NumPy оказалась крайне полезной в целом ряде задач. И это мы рассмотрели далеко не все ее возможности. В качестве источников дополнительной информации можно порекомендовать книги, NumPy их посвящено больше одной. Я лично читал «NumPy Beginners Guide, Third Edition» за авторством Ivan Idris, она оказалась вполне приличной.
Считается, что NumPy потребляет меньше памяти и работает до 10 раз быстрее аналогичного кода, написанного на Python. В этом посте я решил не приводить никаких бенчмарков, потому что тут есть масса нюансов, и все сильно зависит от специфики конкретного приложения (объемы данных, размеры мыссивов, и т.д.). Заинтересованные читатели могут изучить вопрос о производительности NumPy в качестве домашнего задания.
Еще в качестве домашнего задания рекомендую взять два сигнала, один с частотой 250 Гц, и второй с частотой 50 Гц. Перемножьте эти сигналы. Как выглядит FFT результата? Как он изменяется при изменении частоты перемножаемых сигналов? За основу возьмите последний из приведенных скриптов.
Дополнение: Еще примеры использования NumPy вы найдете в статьях Передача изображений в SSB-сигнале с помощью Python и Рисуем диаграммы Вольперта-Смита на Python. Кое-какие пояснения по поводу работы преобразования Фурье вы найдете в Шпаргалке по математике, связанной с I/Q-сигналами и Шпаргалке по работе DSP фильтров.