Пример использования генетических алгоритмов
8 ноября 2010
В этой заметке вы найдете пример практического применения генетических алгоритмов. Предполагается, что вы уже в курсе, что это такое, или по крайней мере прочитали соответствующую статью в Википедии.
Постановка задачи следующая. Есть множество точек, принадлежащих графику некой функции. Нужно найти полином N-ой степени, проходящий как можно ближе к этим точкам. Другими словами, нужно аппроксимировать функцию. Где-то мы это уже видели, правда?
Сплайны — это, конечно, хорошо, но мир клином на них не сошелся. Представьте, что нам нужно аппроксимировать функцию стандартного нормального распределения, чтобы не хранить в программе заранее рассчитанные координаты четырех сотен точек.
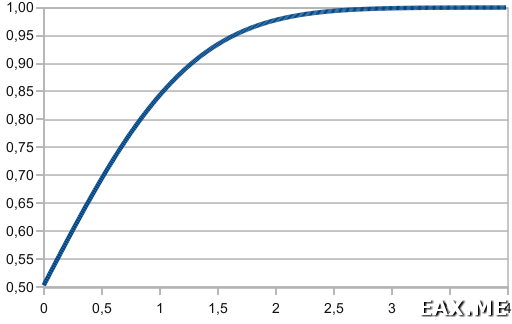
Сплайны в этом случае будут неэффективны. Какая разница, что хранить — координаты всех точек или коэффициенты сотни полиномов 4-ой степени? Можно проигнорировать часть точек, но тогда пострадает точность аппроксимации, а выигрыш в объеме хранимых данных все равно будет невелик.
Генетические алгоритмы позволяют подобрать коэффициенты одного полинома таким образом, чтобы его график проходил максимально близко к графику аппроксимируемой функции. Вот программа на языке Perl, предназначенная для поиска таких полиномов.
# аппроксимация функции с помощью полинома степени MAX_POWER
# поиск коэффициентов производится генетическим алгоритмом
# (c) Alexandr A Alexeev 2010 | http://eax.me/
use strict;
# аппроксимируем функцию полиномом ___ степени
use constant MAX_POWER => 4;
# сколько особей отбираем в каждом поколении
use constant BEST_CNT => 64;
# используем каждую ___ точку
use constant POINT_USE_FREQ => 1;
# загружаем координаты точек аппроксимируемой функции
my %f_tbl;
my $fname = shift;
die "Usage: $0 fname.csv\n" unless($fname);
open FID, "<", $fname;
my $t;
while(<FID>) {
if(++$t == POINT_USE_FREQ) {
$t = 0;
chomp;
my($x, $y) = split/\;/;
$f_tbl{$x} = $y;
}
}
close FID;
# $p[i]->{data} = [a0, a1, a2, ...]
# $p[i]->{rslt} = f
my @p;
# нулевое поколение
for(0..BEST_CNT-1) {
my @t;
push @t, 100 - rand(200) for(0..MAX_POWER);
push @p, { data => \@t };
}
my $gen = 0; # номер поколения
$p[0]->{rslt} = 10; # для входа в цикл
# поиск коэффициентов с помощью ГА
while($p[0]->{rslt} >= 0.0001) {
$gen++;
# 1. -------- скрещивание + мутации --------
for my $i (0..BEST_CNT-2) {
for my $j($i+1..BEST_CNT-1) {
my @t;
# скрещивание
push @t, ($p[$i]->{data}[$_] + $p[$j]->{data}[$_])/2
for(0..MAX_POWER);
# 50% потомства - мутанты
if(rand() < 0.5) {
$t[$_] += $t[$_]*(4-rand(8))
for(0..MAX_POWER);
}
push @p, { data => \@t };
}
} # for ...
# предки вымирают
shift @p for(0..BEST_CNT-1);
# -------- 2. селекция --------
my $n_items = scalar @p;
# вычисляем значения целевой функции
$p[$_]->{rslt} = rslt_f($p[$_]->{data})
for(0..$n_items-1);
# сортируем особей по значению целевой функции
@p = sort { $a->{rslt} <=> $b->{rslt} } @p;
# отбираем лучших особей
my @next_p;
push @next_p, $p[$_] for(0..BEST_CNT-1);
@p = @next_p;
# выводим номер поколения и значение
# целевой функции у "лучшего" потомка
print $gen.";".$p[0]->{rslt}.";";
# выводим формулу для OpenOffice
my $i = 0;
for(@{$p[0]->{data}}) {
my $str = sprintf "%.05f", $_;
$str =~ s/\./\,/;
my $sign = $str =~ /^-/ ? "" : "+";
if($i > 0) {
print $sign;
$str .= $i == 1 ? "*A2" : "*POWER(A2;$i)";
}
$i++;
print $str;
}
print "\n";
}
# функция приспособленности
sub rslt_f {
my ($aref) = @_;
my $max_delta = 0;
for my $x(keys %f_tbl) {
my $delta = abs($f_tbl{$x} - calc_f($aref, $x));
$max_delta = $delta > $max_delta ? $delta : $max_delta;
}
return $max_delta;
}
# вычисление функции-аппроксимации
# в точке x при заданных коэффициентах
sub calc_f {
my ($aref, $x) = @_;
my $rslt;
for(0..MAX_POWER) {
$rslt += $aref->[$_]*($x ** $_);
}
return $rslt;
}
В качестве аргумента скрипт принимает имя файла, состоящего из строк с координатами точек:
0.01;0.5040
0.02;0.5080
0.03;0.5120
0.04;0.5160
0.05;0.5199
0.06;0.5239
0.07;0.5279
0.08;0.5319
0.09;0.5359
0.10;0.5398
0.11;0.5438
0.12;0.5478
...
Роль ДНК в генетическом алгоритме играет массив из MAX_POWER+1 чисел — это коэффициенты полинома. Приспособленность особи определяется, как максимальное отклонение графика полинома от графика аппроксимируемой функции. Чем меньше отклонение, тем более приспособленной считается особь. В скрещивании принимают участие BEST_CNT наиболее приспособленных особей. При скрещивании коэффициенты потомка вычисляются, как среднее арифметическое коэффициентов родителей. 50% потомства мутирует — к каждому коэффициенту прибавляется случайное число, лежащее где-то в диапазоне от -4 до +4 умножить на коэффициент.
На подбор алгоритма у меня ушло несколько часов. Думаю, у людей, более часто работающих с ГА на такие вещи уходит от силы минут 15. С помощью приведенного скрипта мне удалось найти полином, аппроксимирующий функцию стандартного нормального распределения на отрезке [0;4] с погрешностью не более 0,0048:
Φ(x) ~ 0.4953 + 0.461 · x − 0.12472 · x2 + 0.00499 · x3 + 0.001335 · x4
при этом:
Φ(x) = 1 − Φ(−x)
Φμ,σ(x) = Φ((x − μ) / σ)
Последняя формула — для нормального распределения с мат ожиданием μ и дисперсией σ2.
Только подумайте — никаких таблиц, никаких экспонент и интегралов! Все, что нам нужно — это 5 чисел, 4 операции сложения и 7 операций умножения. Всего одна строчка кода на любом процедурном языке программирования. Погрешность менее одной сотой!
Хотите другую функцию? Пожалуйста — вот вам синус на интервале [0; pi/2] с погрешностью 0.00013:
sin(x) ~ 0.00014 + 0.99614 · x + 0.01973 · x2 − 0.20319 · x3 + 0.02855 · x4
Чтобы добиться такой же точности с помощью ряда Тейлора, нужно использовать многочлен 5-ой степени. Тем не менее, для синусов, косинусов, экспонент и логарифмов, наверное, ряды все-таки лучше подходят — и формулы короче и погрешность не такая уж большая.
Дополнение: Простая и эффективная (параллелизуемая) реализация генетического алгоритма на Haskell
Метки: Perl, Алгоритмы, Искусственный интеллект.
Вы можете прислать свой комментарий мне на почту, или воспользоваться комментариями в Telegram-группе.